EDP Sciences logo
Submit your paper
Search
Menu
Home All issues Volume 188 / No 6 (2017) Bull. Soc. géol. Fr., 188 6 (2017) 37 Full HTML
Open Access
Issue
Bull. Soc. géol. Fr.
Volume 188, Number 6, 2017
Article Number 37
Number of page(s) 8
DOI https://doi.org/10.1051/bsgf/2017202
Published online 13 December 2017

© B.C. Vendeville et al., Published by EDP Sciences 2017

Licence Creative CommonsThis is an Open Access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

1 Introduction

It is not uncommon for a fold-and-thrust belt or an accretionary prism to reach, as it propagates toward the foreland, an area in which the sedimentary cover comprises an additional décollement made of evaporites (e.g., salt) or overpressured shale (Fig. 1). This is the case, amongst others, of the Southern and Northern Pyrenees in Spain and France (Vergés et al., 1992; Munoz, 2002; Serrano et al., 2006), the Kuqa Basin in China (Chen et al., 2004), the Mediterranean Ridge (Reston et al., 2002), or the Franklin Mountains in NW Canada (Aitken and Pugh, 1984; Morrell, 1995). In these examples, the thrusts affecting the deeper part of the series do not appear to have propagated much forward, even if the basal décollement extend all across, whereas the frontal basal thrust ramped up and connected within the overlying décollement. Meanwhile, the front of the thin-skinned suprasalt deformation propagated much faster and farther ahead. In the case of the Pyrenees, the deeper décollement pinched out southward and forward propagation of deformation occurred on the upper décollement (Vergés et al., 1992; Santolaria et al., 2015).

We undertook a series of systematic experiments in order to better understand how thick-skinned shortening could interact and, possibly, be influenced by shallow deformation above a silicone layer (to which, we will refer to as “salt” for sake of simplicity) embedded within the sedimentary cover. Similar experiments have already been published (Mugnier et al., 1997; Leturmy et al., 2000; Bonini, 2003; Duerto and McClay, 2009), all of them focusing on how deformation at depth may influence the behavior of the salt and its sediment overburden. However, in the course of our experimental work, we discovered that the presence of salt in the sedimentary cover could, in turn, influence the kinematic evolution of the underlying thrusts sheets at depth. In this article, we present our experimental results, then we discuss the mechanical reasons on how and why such an influence can take place.

thumbnail Fig. 1

Schematic N-S cross section across the Spanish Pyrenees by Larrasoaña et al. (2003), (modified by Santolaria et al., 2015) illustrating a deep-seated Triassic décollement branching out upward into a Eocene evaporitic level.

2 Experimental design and procedure

We designed a series of experiments specifically aimed at better understanding the impact of the presence of a salt layer on the evolution of the deeper thrusts. Here, we present only the three most significant ones. All models were made mostly of dry quartz sand (angle of internal friction: 30–34°) (Klinkmüller et al., 2016) and had an initial length of 121 cm, and an initial total thickness of 28 mm (lower and upper series) resting on a 2 mm thick layer of glass microbeads, which acted as a deep frictional basal detachment (Fig. 2). Some models included a salt-analogue layer (viscous silicone polymer SGM 36, having a viscosity of about 2 x 104 Pa.s) (Rudolf et al., 2016) embedded at mid height within the cover, whereas others did not. All models were deformed at a rate of 0.47 cm/h (corresponding to about few cm/yr in nature) until a total amount of shortening of 54.6 cm was reached (55%).

The first two models (Models 1 and 2) were built in a cylindrical fashion. Model 1 comprised of only one single, 28-mm-thick layer of dry sand lying across the entire model (Fig. 2, top) overlying a 2 mm-thick glass microbead-glass layer. Model 2 included a 5 mm thick layer of viscous silicone. This layer overlaid a 13-mm-thick lower sand layer and was overlain by a 10 mm thick brittle sand cover (Fig. 2, middle). The viscous silicone layer covered only part of the model's length but lay all across the entire model's width (Fig. 2, middle). It is worth noting that previous models in the literature generally display boundary conditions in which an interbedded viscous level is in direct contact with the backstop at the initial stage (Guillier et al., 1995; Leturmy et al., 2000; Bonini, 2003; Sherkati et al., 2006; Nilfouroushan et al., 2012; Ruh et al., 2012). Very few experiments and numerical simulations started with a frictional domain between the backstop and the interbedded viscous level (e.g. Cotton and Koyi 2000, Costa and Vendeville 2002, Stockmal et al., 2007, Yin et al., 2011). In the latter cases, the frictional domain along the backstop was narrow, in the range of 5–10 cm. In Model 2, the frictional internal domain was 60 cm long, which allowed for building a mature wedge before deformation reached the viscous silicone domain.

Finally, the design for Model 3 was more three-dimensional, as it included one lateral half that comprised an interbedded silicone layer, and one other half that has sand only (Fig. 2, bottom). In models that comprised a salt-analogue décollement (Models 2 and 3), we reduced the lateral friction between the upper sand layers and the lateral vertical glass walls by inserting a thin, vertical film of silicone between the sidewalls and the model itself (as in Costa and Vendeville, 2002; Couzens-Schultz et al., 2003; Santolaria et al., 2015).

thumbnail Fig. 2

Initial geometry of Models 1, 2 and 3. The cross sections are vertically exaggerated 4:1.

3 Terminology

Figure 3 illustrates, for the sake of clarity, what we mean below in terms of shallow and deep thrusts. The deep thrusts root at depth into the lower décollement made of frictional glass microbeads. In contrast, the shallow or upper thrusts root into the viscous silicone layer embedded at mid height of the sedimentary cover.

thumbnail Fig. 3

Schematic cross sections indicating the terminology we use for deep and shallow thrusts in our discussion.

4 Experimental results

Model 1, having only one potential frictional décollement at depth, deformed in a manner similar to previously published “classic” models of fold-and-thrust belts and accretionary prisms (Malavieille, 1984; Mulugeta and Koyi, 1987, and many authors), with a stable critical taper of about 8–10°, and younger thrusts forming ahead of older ones, in a piggy-back fashion (Figs. 4A, 5A, and 6).

Model 2 had two distinct stages of evolution. First, the model evolved as Model 1 until the deformation front reached the hinterland pinch-out of the salt-bearing domain (formation of Thrust 6 in Figs. 4B, 5B, and 6). From that stage on, in the upper part of the overburden, the deformation front propagated forward fast (Thrusts 7 to 9 in Figs. 4B and 5B) and rapidly reached the foreland salt pinch out (as in Costa and Vendeville, 2002; Santolaria et al., 2015). However, at depth, no new thrust formed. The deep fold-and-thrust belt stopped propagating forward (Figs. 5B and 6), and all further shortening was accommodated by an unusually large amount of slip along Thrust 6 (which slid on the shallow salt weld; Figs. 5B and 6), and, to a less extent, by reactivating older thrusts (1 to 5 in Fig. 5B). With no doubt, the presence of a salt layer in the cover blocked the forward propagation of the deep fold-and-thrust belt. In addition, the overall surface slope angle (resulting from movement along both the upper and deep structures) was much lower than that in Model 1. Also, there is a sharp contrast in taper between the proximal area devoid of salt (a few degrees) and the distal area where salt was present (near zero degree).

In Model 3 (Fig. 4C, 5C and D, and Fig. 6), which had two different lateral compartments, the structural evolution varied along strike, and some amount of lateral influence occurred between the two compartments. In Model 3, just as in Model 2, the kinematics in both the upper and deeper series changed radically once the deformation front reached the salt-bearing region. As in Model 2, deformation in the upper series propagated forward fast. At the same time, in the deeper series, the forward propagation of the deformation front slowed down dramatically in both the North (no salt; Fig. 5) and South (salt-bearing) regions (Figs. 4C and Fig. 6). As in Model 2, it is the foremost thrust (here, Thrust 5 in Figs. 5D and 6) that accommodated most of the displacement, although one late thrust (Thrust 13) formed during the very latest stages of the experiment (Figs. 5D and 6). Laterally, this influenced the salt-free area by forcing the foremost basement thrust (Thrust 5 in Figs. 5C and 6) to remain active longer than usual before being replaced by Thrust 13.

thumbnail Fig. 4

Overhead photographs of Models 1, 2 and 3 during deformation, all at the same scale. The area comprising a salt-analogue décollement is outlined by white dashed lines. Black lines indicate the location of the cross sections shown in Figure 5. "S" stands for "shortening".
thumbnail Fig. 5

Cross sections in all three models after deformation. Figures 5C and D are located outside and inside, respectively the salt-bearing area in Model 3. The blue dashed lines mark the initial position of the internal and external salt pinch outs. Figure 5E compares the topographic profiles of the two sections of Model 3 (Red: salt-bearing region; Blue: Salt-free region).
thumbnail Fig. 6

Chart indicating the total displacement along each, basal, sub-salt thrust in each model (and two for Model 3, one in the frictional region, one in the viscous region). The chart illustrates that, at the final stage, fewer new thrusts formed when a viscous layer was interbedded in the cover. It also shows a similar pattern during the first part of the experiment, then a significant increase in total displacement along the frontal thrust once the front reached the area comprising an interbedded viscous layer (Thrust 6 in Model 2, Thrust 5 in Model 3). Note that even in the frictional half of Model 3, Thrust 5 had a significantly larger displacement than in the salt-free model (Model 1), which illustrates the lateral influence on the frictional region of the adjacent salt-bearing region.

5 Discussion / Conclusions

The crucial observation about the evolution of the salt-bearing models described above is that forward propagation of the deep thrust front is stopped, or at least drastically slowed down, once the deformation front reaches the hinterland salt pinch out. This pattern is well illustrated by the chart in Figure 6: before the deep deformation reaches the proximal salt pinch out, most of the thrusts have the same behavior and overall slip. From that stage on, even though deformation in the upper series propagates rapidly forward and quickly reaches the external salt pinch out, forward propagation of the deep deformation front appears to come to a stand still, and there, most of the subsequent regional shortening is accommodated, not by forming new thrusts ahead, but by continued long-lasting slip along the foremost deep thrust, and by reactivating the other thrusts. This, in turns allows for the vertical stacking of basement thrusts behind the hinterland salt pinch out. In another article (Borderie et al., 2018), we illustrate what would be the further evolution of such a system, a system where deformation in the hinterland progresses much longer, then all new basal thrusts are shorter and stack vertically one above the other, leading to a geometry similar to that of an asymmetric anticlinal stack.

Simple mechanical considerations can help explain this change in behavior. The ability of a fold-and-thrust belt to propagate forward depends on its capacity to build up enough gravitational energy by creating a surface slope in order to overcome the various stresses that resist its advance. In purely 2-D systems, such resistance comes only from the friction / shear stress resistance exerted at the base of the system (Chapple, 1978; Suppe, 1981; Davis et al., 1983; Dahlen, 1990), and additional stresses if the detachment system is not horizontal (e.g., Koyi and Vendeville, 2003). Where the fold-and-thrust belt detaches on an evaporitic layer, rocksalt's viscosity is so low that the critical surface slope is very gentle, near zero or so (Davis and Engelder, 1985; Cotton and Koyi, 2000; Costa and Vendeville, 2002; Storti et al., 2007), and the deformation front can rapidly propagate across the entire basin and reach the foreland salt pinch out.

In our models, the critical taper that was needed for the deep fold-and-thrust belt to propagate was about 8 to 10° (based on Model 1's results). It is this topographic slope that allowed deformation to propagate forward. However, as soon as the deformation front reached the area where salt was present (Models 2 and 3), the overall topographic slope was no longer controlled by the ideal critical taper observed in the proximal region, but by that of the salt-bearing region. This means that the critical taper was much lower than that required for the deep fold-and-thrust belt to propagate. How the presence of a viscous décollement within the cover can affect a fold-and-thrust belt's topography is illustrated by the two profiles in Figure 5E, and also by a frontal photograph of Model 3 (Fig. 7). On this photograph, the topography in the salt-free area (left-hand side) is much higher than that in the salt-bearing region (right-hand side), as highlighted by the white topographic line.

In response to the lowering of the regional topographic slope once the deformation front reached the salt province, the deeper belt was no longer capable of propagating forward. Instead, it accommodated further shortening by continually activating the youngest thrust and by thickening the entire wedge behind. It has to be noted that the change in the slope angle is very abrupt and remains so even once the deep frontal thrust has ramped up to the salt-bearing décollement.

In some way, the influence of having salt within the cover is analogous to that of surface processes, such as erosion or sedimentation, that can alter the overall topographic slope (Konstantinovskaia and Malavieille, 2005; Graveleau et al., 2012) and can thereby impact the behavior of the underlying thrusts.

In other words, by imposing a low topographic taper, the presence of a salt décollement makes the forward propagation of the deep fold-and-thrust belt much more difficult, if not impossible and it does even influence the kinematics of thrusts located laterally outside the salt-bearing region.

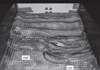thumbnail Fig. 7

Frontal view of Model 3 (looking toward the backstop). The left-hand side region has no viscous décollement, whereas the right-hand side region comprises a viscous décollement embedded within the cover. Note the marked lateral change in topographic elevation across the model's width (thick white line). The scale is indicated by the 1.5 cm x 1.5 cm passive markers printed on the model's surface.

Supplementary Material

The data files related to this manuscript are 6 short movie files from each of the three models showing their evolution in map and side views. Access here

Acknowledgments

This work was funded by the Tarim Oilfied Company (Korla, China), a subsidiary of Petrochina. We also thank numerous colleagues for fruitful discussions, and two anonymous reviewers for their helpful comments.

References

  • Aitken JD, Pugh DC. 1984. The Fort Norman and Leith Ridge structures; major, buried, Precambrian features underlying Franklin Mountains and Great Bear and Mackenzie plains. Bulletin of Canadian Petroleum Geology 32 (2): 139–146. [Google Scholar]
  • Bonini M. 2003. Detachment folding, fold amplification, and diapirism in thrust wedge experiments. Tectonics 22 (6): 1065. [CrossRef] [Google Scholar]
  • Borderie S, Graveleau F, Witt C, Vendeville BC. 2018. Impact of an interbedded viscous décollement on the structural and kinematic coupling in fold-and-thrust belts: Insights from analogue modeling. Tectonophysics 722: 118–137 (in press). [Google Scholar]
  • Chapple WM. 1978. Mechanics of thin-skinned fold-and-thrust belts. Geological Society of America Bulletin 89 (8): 1189–1198. [CrossRef] [Google Scholar]
  • Chen S, Tang L, Jin Z, Jia C, Pi X. 2004. Thrust and fold tectonics and the role of evaporites in deformation in the Western Kuqa Foreland of Tarim Basin, Northwest China. Marine and Petroleum Geology 21 (8): 1027–1042. [CrossRef] [Google Scholar]
  • Costa E, Vendeville BC. 2002. Experimental insights on the geometry and kinematics of fold-and-thrust belts above a weak, viscous evaporite décollement. Journal of Structural Geology 24 (11): 1729–1739. [CrossRef] [Google Scholar]
  • Cotton J, Koyi H. 2000. Modeling of thrust fronts above ductile and frictional detachments: application to structures in the Salt Range and Potwar Plateau, Pakistan. Geological Society of America Bulletin 112 (3): 351–363. [CrossRef] [Google Scholar]
  • Couzens-Schultz BA, Vendeville BC, Wiltschko DV. 2003. Duplex style and triangle zone formation: insights from physical modeling. Journal of Structural Geology 25 (10): 1623–1644. [CrossRef] [Google Scholar]
  • Dahlen FA. 1990. Critical taper model of fold-and-thrust belts and accretionary wedges. Annual Review of Earth and Planetary Sciences 18: 55–99. [CrossRef] [Google Scholar]
  • Davis D, Suppe J, Dahlen FA. 1983. Mechanics of fold-and-thrust belts and accretionary wedges. Journal of Geophysical Research 88 (B12): 1153–1172. [CrossRef] [Google Scholar]
  • Davis DM, Engelder T. 1985. The role of salt in fold-and-thrust belts. Tectonophysics 119 (1–4): 67–88. [CrossRef] [Google Scholar]
  • Duerto L, McClay K. 2009. The role of syntectonic sedimentation in the evolution of doubly vergent thrust wedges and foreland folds. Marine and Petroleum Geology 26 (7): 1051–1069. [CrossRef] [Google Scholar]
  • Graveleau F, Malavieille J, Dominguez S. 2012. Experimental modelling of orogenic wedges: A review. Tectonophysics 538–540: 1–66. [CrossRef] [Google Scholar]
  • Guillier B, Baby P, Colletta B, Mendez E, Limachi R, Letouzey J, Specht M. 1995. Analyse géométrique et cinématique d'un “duplex” issu d'un modèle analogique visualisé en 3D par tomographie aux rayons X. Comptes Rendus de l'Académie des Sciences − Series IIA − Earth and Planetary Science Série 2a: Sciences de la Terre (321): 901–908. [Google Scholar]
  • Klinkmüller M, Schreurs G, Rosenau M, Kemnitz H. 2016. Properties of granular analogue model materials: A community wide survey. Tectonophysics 684: 23–38. [CrossRef] [Google Scholar]
  • Konstantinovskaia E, Malavieille J. 2005. Erosion and exhumation in accretionary orogens: Experimental and geological approaches. Geochemistry, Geophysics, and Geosystems 6 (Q02006). [CrossRef] [Google Scholar]
  • Koyi HA, Vendeville BC. 2003. The effect of décollement dip on geometry and kinematics of model accretionay wedges. Journal of Structural Geology 25 (9): 1445–1450. [CrossRef] [Google Scholar]
  • Larrasoaña JC, Pares JM, Millan H, del Valle J, Pueyo EL. 2003. Paleomagnetic, structural and stratigraphic constraints on tranverse fault kinematics during basin inversion: the Pamplona Fault (Pyrenees, north Spain). Tectonics 22 (1071). [Google Scholar]
  • Leturmy P, Mugnier JL, Vinour P, Baby P, Colletta B, Chabron E. 2000. Piggyback basin development above a thin-skinned thrust belt with two detachment levels as a function of interactions between tectonic and superficial mass transfer: the case of the Subandean Zone (Bolivia). Tectonophysics 320 (1): 45–67. [CrossRef] [Google Scholar]
  • Malavieille J. 1984. Modélisation expérimentale des chevauchements imbriqués: application aux chaînes de montagnes. Bulletin de la Société Géologique de France 7 (1): 129–138. [CrossRef] [Google Scholar]
  • Morrell. 1995. Petroleum Exploration in Northern Canada: A Guide to Oil and Gas Exploration and Potential. N. O. a. G. D. I. a. N. A. Canada: 117. [Google Scholar]
  • Mugnier JL, Baby P, Colletta B, Vinour P, Bale P, Leturmy P. 1997. Thrust geometry controlled by erosion and sedimentation: a view from analogue models. Geology 25 (5): 427–430. [CrossRef] [Google Scholar]
  • Mulugeta G, Koyi H. 1987. Three-dimensional geometry and kinematics of experimental piggyback thrusting. Geology 15 (11): 1052–1056. [CrossRef] [Google Scholar]
  • Munoz JA. 2002. Alpine tectonics I: the Alpine system north of the Betic Cordillera tectonic setting; the Pyrenees. In : Gibbons Z, Moreno T, The Geology of Spain. London: Geological Society, pp. 370–385. [Google Scholar]
  • Nilfouroushan F, Pysklywec R, Cruden A. 2012. Sensitivity analysis of numerical scaled models of fold-and-thrust belts to granular material cohesion variation and comparison with analog experiments. Tectonophysics 526–529: 196–206. [CrossRef] [Google Scholar]
  • Reston TJ, Fruehn J, von Huene R. 2002. The structure and evolution of the western Mediterranean Ridge. Marine Geology 186 (1–2): 83–110. [CrossRef] [Google Scholar]
  • Rudolf M, Boutelier D, Rosenau M, Schreurs G, Oncken O. 2016. Rheological benchmark of silicone oils used for analog modeling of short- and long-term lithospheric deformation. Tectonophysics 684: 12–22. [CrossRef] [Google Scholar]
  • Ruh JB, Kaus BJP, Burg J.-P. 2012. Numerical investigation of deformation mechanics in fold-and-thrust belts: Influence of rheology of single and multiple décollements. Tectonics 31 (3). [Google Scholar]
  • Santolaria P, Vendeville BC, Graveleau F, Soto R, Casas-Sainz A. 2015. Double evaporitic décollements: Influence of pinch-out overlapping in experimental thrust wedges. Journal of Structural Geology 76 (0): 35–51. [CrossRef] [Google Scholar]
  • Serrano O, Delmas J, Hanot F, Vially R, Herbin J.-P, Houel P, Tourlière B. 2006. Le Bassin d'Aquitaine: valorisation des données sismiques, cartographie structurale et potentiel pétrolier. BRGM. [Google Scholar]
  • Sherkati S, Letouzey J, Frizon de Lamotte D. 2006. Central Zagros fold-thrust belt (Iran): New insights from seismic data, field observation, and sandbox modeling. Tectonics 25 (4). [Google Scholar]
  • Stockmal GS, Beaumont C, Nguyen M, Lee B. 2007. Mechanics of thin-skinned fold-and-thrust belts: insights from numerical models. Whence the mountains? Inquiries into the evolution of orogenic systems: a volume in honor of Raymond A. Price. J. W. Sears, T. A. Harms and C. A. Evenchick (Boulder, CO, USA), Geological Society of America Special Paper. 433: 63–98. [Google Scholar]
  • Storti F, Soto Marín R, Rossetti F, Casas Sainz AM. 2007. Evolution of experimental thrust wedges accreted from along-strike tapered, silicone-floored multilayers. Journal of the Geological Society, London 164: 73–85. [CrossRef] [Google Scholar]
  • Suppe J. 1981. Mechanics of mountain building and metamorphism in Taiwan. Memoir of the Geological Society of China 4: 67–89. [Google Scholar]
  • Vergés J, Martínez A, Muñoz JA. 1992. South Pyrenean fold and thrust belt: The role of foreland evaporitic levels in thrust geometry. In : McClay KR, Thrust Tectonics. Chapman & Hall, 255–264. [CrossRef] [Google Scholar]
  • Yin H, Wang Z, Wang X, Wu Z. 2011. Characteristics and mechanics of Cenozoic salt-related structures in Kuqa foreland basin: insights from physical modeling and discussion. Geological Journal of China Universities 17 (2): 308–317. [Google Scholar]

Cite this article as: Vendeville BC, Pengcheng T, Graveleau F, Shaoying H, Wang X. 2017. How the presence of a salt décollement in the sedimentary cover influences the behavior of subsalt thrusts in fold-and-thrust belts, Bull. Soc. géol. Fr. 188: 37.

All Figures

thumbnail Fig. 1

Schematic N-S cross section across the Spanish Pyrenees by Larrasoaña et al. (2003), (modified by Santolaria et al., 2015) illustrating a deep-seated Triassic décollement branching out upward into a Eocene evaporitic level.
In the text
thumbnail Fig. 2

Initial geometry of Models 1, 2 and 3. The cross sections are vertically exaggerated 4:1.
In the text
thumbnail Fig. 3

Schematic cross sections indicating the terminology we use for deep and shallow thrusts in our discussion.
In the text
thumbnail Fig. 4

Overhead photographs of Models 1, 2 and 3 during deformation, all at the same scale. The area comprising a salt-analogue décollement is outlined by white dashed lines. Black lines indicate the location of the cross sections shown in Figure 5. "S" stands for "shortening".
In the text
thumbnail Fig. 5

Cross sections in all three models after deformation. Figures 5C and D are located outside and inside, respectively the salt-bearing area in Model 3. The blue dashed lines mark the initial position of the internal and external salt pinch outs. Figure 5E compares the topographic profiles of the two sections of Model 3 (Red: salt-bearing region; Blue: Salt-free region).
In the text
thumbnail Fig. 6

Chart indicating the total displacement along each, basal, sub-salt thrust in each model (and two for Model 3, one in the frictional region, one in the viscous region). The chart illustrates that, at the final stage, fewer new thrusts formed when a viscous layer was interbedded in the cover. It also shows a similar pattern during the first part of the experiment, then a significant increase in total displacement along the frontal thrust once the front reached the area comprising an interbedded viscous layer (Thrust 6 in Model 2, Thrust 5 in Model 3). Note that even in the frictional half of Model 3, Thrust 5 had a significantly larger displacement than in the salt-free model (Model 1), which illustrates the lateral influence on the frictional region of the adjacent salt-bearing region.
In the text
thumbnail Fig. 7

Frontal view of Model 3 (looking toward the backstop). The left-hand side region has no viscous décollement, whereas the right-hand side region comprises a viscous décollement embedded within the cover. Note the marked lateral change in topographic elevation across the model's width (thick white line). The scale is indicated by the 1.5 cm x 1.5 cm passive markers printed on the model's surface.
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.