| Issue |
BSGF - Earth Sci. Bull.
Volume 192, 2021
|
|
|---|---|---|
| Article Number | 10 | |
| Number of page(s) | 13 | |
| DOI | https://doi.org/10.1051/bsgf/2020049 | |
| Published online | 23 March 2021 | |
FMHex20: An earthquake focal mechanism database for seismotectonic analyses in metropolitan France and bordering regions
1
Géosciences Montpellier, CNRS, Université de Montpellier, Université des Antilles,
Montpellier, France
2
CEA DAM Ile-de-France,
Bruyères-le-Châtel, France
3
Géoazur, Université Côte d’Azur, CNRS, Observatoire de la Côte d’Azur, IRD,
Valbonne, France
4
Institut Terre Environnement Strasbourg, École et Observatoire des Sciences de la Terre, CNRS, Université de Strasbourg,
Strasbourg, France
5
Bureau d’Evaluation des Risques Sismiques pour la Sûreté des Installations, Institut de Radioprotection et Sûreté Nucléaire,
Fontenay-aux-Roses, France
6
Institut de Recherche en Astrophysique et Planétologie, CNRS, UPS, CNES, Université de Toulouse,
Toulouse, France
* Corresponding author: stephane.mazzotti@umontpellier.fr
Received:
27
April
2020
Accepted:
21
December
2016
We present a compilation of over 1700 focal mechanisms for nearly 1300 earthquakes in metropolitan France and bordering regions of Western Europe. It is based on both published and unpublished sources (articles, reports, observatory websites) for which the focal mechanism solutions have been verified for internal consistency, corrected in cases of minor errors and rejected in cases of major inconsistencies between the parameters. The database, labeled FMHex20, is a first version and should be regularly updated in the future as part of an ongoing effort within the Seismicity Transverse Action of the French Résif research infrastructure. We also present first-order seismotectonic analyses for the whole metropolitan France and for two regions (Western France and Northern Alps-Jura-Vosges) to illustrate how the FMHex20 database can serve as a basis for geodynamic or seismic hazard zonation studies. Combined with complementary datasets, it can improve our understanding of the kinematics of potentially active faults, including in very-low-strain-rate regions as is the case for most of France.
Key words: Focal mechanism / earthquake / seismotectonics / metropolitan France
© S. Mazzotti et al., Published by EDP Sciences 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The characterization of earthquake sources using focal mechanisms – also called fault plane solutions – is concomitant with the development of modern seismology in the 1950s and the installation in the 1960s of the World-Wide Standardized Seismograph Network that allowed computations of focal mechanisms for large earthquakes everywhere on the globe (e.g., Byerly and Stauder, 1958; Stauder, 1962). These proved an important dataset in the development of the Plate Tectonics framework (Sykes, 1967). Since then, earthquake focal mechanisms are used in most studies of active tectonics, from individual fault mechanics to regional dynamics (e.g., Hardebeck and Michael, 2004; Stich et al., 2006), including in the construction of seismotectonic models for seismic hazard assessments (e.g., Cushing et al., 2007; Vanneste et al., 2013).
In this article, we present a database of 1733 focal mechanisms for 1290 individual earthquakes in metropolitan France and bordering regions of Western Europe based on the compilation of solutions from published articles, unpublished reports and online publications of seismological agencies. The database, labeled FMHex20 (Focal Mechanisms of Hexagon 2020), represents the first realization of the compilation, with an objective of regular updates within the Seismicity Transverse Action of the French Résif (“Réseau Sismologique et Géodésique Français”) research infrastructure.
We first present in Section 2 a short review of previous studies that illustrate the current knowledge on focal mechanisms and state of stress in France, with a description of the main limitations on focal mechanism estimations. The FMHex20 database is described in Section 3, including the presentation of the sources, database format and processing. In particular, we present the procedures used for identification and correction of erroneous data, and for estimating the variability between multiple mechanism solutions for the same earthquake. Finally, a short discussion of the French national and regional seismotectonics is presented in Section 4 using first-order analyses of the new database. This last section illustrates the importance of focal mechanisms to better understand the complex patterns and processes related to active deformation, seismotectonics and seismic hazard in various regions of metropolitan France.
Hereafter, earthquake magnitudes are noted Mw when referring to moment magnitudes and M for all other undifferentiated magnitudes (ML, MS, mb, etc.). For detailed information on focal mechanism computation, the reader is referred to method publications such as Dziewonski et al. (1981), Reasenberg and Oppenheimer (1985) or Hardebeck and Shearer (2002).
2 Previous studies and limitations
Early studies of earthquake focal mechanisms in France date from the late 1970s–early 1980s, with applications to the Alps, Pyrenees and Western France (Fréchet and Pavoni, 1979; Godefroy, 1980; Veinante-Delahaye and Santoire, 1980; Dorel et al., 1983). Most of these and of the following studies estimate focal mechanisms from the polarities of direct and refracted P waves (Pg and Pn) at local and regional distances (< 200–300 km). These so-called first-motion solutions provide information on the double-couple component of the mechanism (azimuths and dips of the nodal planes, directions of the slip vectors, azimuths and dips of the compression and tension axes). They are computed for earthquakes of magnitude typically M ≥ 2.0–3.0, depending primarily on the density and azimuthal distribution of the regional seismometer network.
In parallel, since the 1980s–1990s several global and regional projects, such as the European-Mediterranean Regional Centroid Moment Tensor Catalog (Pondrelli et al., 2002), determine focal mechanisms and Mw magnitudes for moderate to large earthquakes (Mw ≥ 4.0–5.0) using time-domain moment tensor inversion of teleseismic and regional waveforms. Owing to the deployment of national broadband networks in the early 2000s, this methodology can be applied for smaller magnitudes (Mw ≥ 3.0–3.5). For earthquakes in France and neighboring regions, computations of moment tensors are performed automatically by regional and national observatories (Delouis, 2014; Rueda and Mezcua, 2005; Scognamiglio et al., 2009), as well as in specific regional studies (e.g., Chevrot et al., 2011).
In the last forty years, numerous studies provide lists of new and compiled earthquake focal mechanisms at regional or national scales. In most cases, the focal mechanism datasets are processed to estimate local or regional mean state of either strain or stress using various techniques such as mechanism summation or stress tensor inversion (e.g., Michael, 1987; Kostrov, 1974; Gephart and Forsyth, 1984; Roselli et al., 2018). The majority is focused on the Alps but most regions of active seismicity are covered (Fig. 1). We present below a very succinct summary of the main results by region, with a non-exhaustive list of associated references:
-
Western France (Armorican Massif, Normandy, northwestern Massif Central): Predominant extension and strike-slip deformation w (σ3) horizontal and oriented roughly NE-SW (Amorèse et al., 2000; Delouis et al., 1993; Mazabraud et al., 2005; Perrot et al., 2005; Veinante-Delahaye and Santoire, 1980).
-
Rhenish Massif and Lower Rhine Graben: Mix of extension and strike-slip deformation, with a minimum principal stress (σ3) horizontal and oriented NNE-SSW (Delouis et al., 1993; Hinzen, 2003; Nicolas et al., 1990).
-
Jura and Upper Rhine Graben: Predominantly strike-slip deformation with a maximum principal stress (σ1) oriented NW-SE (Delouis et al., 1993; Kastrup et al., 2004; Nicolas et al., 1990; Fréchet et al., 2011; Rabin et al., 2018).
-
Alps: Overall orogen-normal extension in the inner (high topography) region and a mix of strike-slip and shortening deformation in the French and Swiss foreland. The minimum (resp. maximum) horizontal stress rotates with the Alps curvature in the extension (resp. shortening) domains (Delacou et al., 2004; Kastrup et al., 2004; Sue et al., 1999).
-
Southwestern Alps and Ligurian Sea: Complex deformation pattern with short spatial variations including extension in the inner (highest topography) region and shortening in the Provence and Italian forelands and the Liguria and Corsica-Sardinia margins (Baroux et al., 2001; Eva et al., 1997; Larroque et al., 2009; Larroque et al., 2016).
-
Pyrenees: Overall orogen-normal extension with lateral variations from transtensive deformation in the East to a mix of extension and local shortening in the West. The minimum principal stress (σ3) is horizontal and oriented in the NE-SW quadrant (Chevrot et al., 2011; Rigo et al., 2015; Sylvander et al., 2008).
Several limitations are associated with regional focal mechanism studies. The most significant source of uncertainty for these small- to moderate-magnitude earthquakes is the spatial distribution of local and regional seismometers. For earthquakes of magnitude M ≈ 2–4, first-motion polarities can only be derived for epicentral distances up to ca. 100–300 km, which strongly limits the number and spatial distribution of useable seismic stations. This issue is especially important for earthquakes near network borders, such as along the Atlantic or Mediterranean margins. It can result in focal mechanisms computed with a small number of polarities (less than 10–15 readings) and azimuthal gaps leading to an incomplete sampling of the focal sphere (Amorèse et al., 2000). The second major source of uncertainty is the seismic velocity model, which impacts both the hypocenter locations and the seismic ray takeoff angles. The impact of the velocity-model uncertainty and spatial variability on focal mechanism computation can be tested to estimate the resulting variability in the mechanism parameters (Amorèse et al., 2000; Mazabraud et al., 2005; Scognamiglio et al., 2016) but, in practice, this source of uncertainty is commonly underestimated (Hardebeck and Shearer, 2002).
In our database, as in other compilations, the heterogeneity of the models and parameters used to compute the focal mechanisms represent an important limitation. Solutions from different studies are based on different velocity models and seismometer networks, leading to different biases on the focal mechanisms that cannot be fully evaluated without recomputing all mechanisms with the same models and parameters. In some cases, the compatibility between different analyses can be estimated, to a first order, by comparing the velocity models and seismometer networks used in each study, but this information is not always reported with the adequate level of detail. This issue is particularly true for the FMHex20 database, which compiles tens of different sources, published and unpublished, over a 30-year period during which the seismic networks and knowledge of the crust and mantle velocity structure have strongly evolved. We partly discuss this limitation in Section 3.2 where we compare multiple solutions from different studies of the same earthquake. Although half of the multiple solutions agree reasonably well (average angular difference < 20°), some earthquakes are associated with very different focal mechanism solutions (average angular difference of 60° or more), illustrating the inconsistencies that can result from different analyses.
 |
Fig. 1 Schematic state of stress in France from published focal mechanism inversions. Thick dashed lines with inward-pointing arrows indicate the general direction of maximum horizontal compressive stress for Western Europe (e.g., Heidbach et al., 2018). Small bars show the orientations of maximum horizontal compressive stress from published regional focal mechanism inversions, with the deformation regime indicated in color: green = strike slip, blue = extension, red = shortening. Numbers indicate the reference for the nearest stress indicator: 1 – Baroux et al. (2001); 2 – Mazabraud et al. (2005); 3 – Rigo et al. (2015); 4 – Sue et al., (1999); 5 – Eva et al. (1997); 6 – Delouis et al. (1993); 7 – Hinzen (2003); 8 – Plenefisch and Bonjer (1997); 9 – Rabin et al. (2018). URG and LRG: Upper and Lower Rhine Graben. |
3 FMHex20 database
FMHex20 is a compilation of focal mechanism solutions from published and unpublished sources, with the references (articles, reports, web pages…) given in the database for each solution. Several of the published articles are themselves based on compilations of previously published and new solutions. In these cases, the user is referred to the referenced article for detailed information on the original solution. Additional solutions are gathered from online sources from seismological institutes in France and Europe, and from unpublished reports from French observatories. Overall, the database comprises focal mechanisms for earthquakes between 1954 and 2019 (plus one event in 1909), ranging in magnitude between M = 0.5 and M = 6.0, and covering metropolitan France and bordering regions (longitude: −6.48°–10.99°; latitude: 40.02°–52.52°). An online version of the database, with data exploration and export options, is available on the OREME Observatory web site (https://data.oreme.org/observation/fmhex).
3.1 Database characteristics and processing
The database consists of a table (in “Comma Separated Value” and “Libre Office” formats) with one line per focal mechanism solution comprising the following information:
-
N: Individual earthquake number (multiple solutions are possible for a single earthquake).
-
Code: Identifier or reference number of the focal mechanism solution in the original source.
-
Year, Month, Day, Hour, Min, Sec: Date and time of the earthquake in the original source.
-
Original Location (Lat0, Lon0, Depth0, Mw0, M0): Location (latitude and longitude in degrees, depth in km) and magnitude (Mw or undifferentiated M) of the earthquake in the original source.
-
SI-Hex Location (LatS, LonS, DepthS, MwS, IDS): Location (latitude and longitude in degrees, depth in km) and magnitude (Mw) of the earthquake in the SI-Hex instrumental catalogue (Cara et al., 2015). NB: This location is for reference only and does not correspond to the one used in the focal mechanism computation.
-
Fault Plane1 and Fault Plane2 (Az1, Dip1, Rake1, Az2, Dip2, Rake2): Azimuths, dips and rakes (in degrees) of the focal mechanism nodal planes (right-hand side convention).
-
P Axis and T Axis (AzP, DipP, AzT, DipT): Azimuths and dips (in degrees) of the focal mechanism P and T axes.
-
DiffP and DiffT: Average P and T axis angular differences between multiple solutions for the same earthquake (cf. Section 3.2).
-
Quality (Q): Three-tier quality factor (A: good, B: average, C: poor) of the focal mechanism solution as provided in the original source or based on an evaluation of the quality/uncertainty in the original source, when available (26% of the database). NB: Due to the disparity between sources, quality estimations are not homogeneous and are only provided as a qualitative guideline.
-
Region: Geographical region indication for metropolitan France.
-
Reference: cf. References.
-
Comments: Potential corrections applied to the focal mechanism solution (see below).
A validation procedure is applied to ensure the internal consistency of the focal mechanism parameters and add missing values when needed. The procedure uses the RFOC package (Lees, 2018) of the R software (R Core Team, 2019) for computation of the parameters. For each solution, the azimuth, dip and rake of the second nodal plane and the azimuths and dips of the P and T axes are computed using the first nodal plane parameters. The computed values are compared to the original ones and the latter are corrected for discrepancies (differences larger than 1 degree) that can be associated with rounding or typographical errors on one or two parameters. The original parameter values are reported in the “Comments” column of the table. Several original solutions involving numerous parameter inconsistencies were noted and excluded from the database as no simple correction could be applied.
In a second phase, all solutions are associated to a unique earthquake number (N) and matched to events in the SI-Hex instrumental catalogue (Cara et al., 2015) when possible. This stage involves identifying multiple solutions for the same earthquake, with a level of uncertainty related to small differences in the original earthquake location parameters. The number of different focal mechanism solutions per earthquake is shown in Figure 2. Out of the 1290 individual earthquakes, over three quarters (1006) are associated with a single solution. Double and triple solutions are the next most frequent (resp. 186 and 65 earthquakes). Earthquakes with 4–9 different solutions only account for a few tens of events.
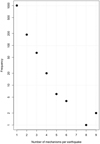 |
Fig. 2 Number of focal mechanism solutions per earthquake. Note the logarithmic scale for the frequencies. |
3.2 Multiple mechanism solutions
Measuring the compatibility between different focal mechanisms is not a straightforward process. Several approaches exist ranging from graphical comparison by superposition of the focal mechanism representations (Amorèse et al., 2000) to geometric comparison of the full moment tensors (Tape and Tape, 2012). In FMHex20, comparisons based on full moment tensors would not be effective because the vast majority of solutions are double-couple mechanisms. In order to estimate the compatibility between multiple mechanisms for a given earthquake, we use an approach based on the angular differences between the P (and T) axes of the compared mechanisms. The angular difference between two axes can vary between 0° (identical vectors) and 90° (orthogonal vectors, maximum incompatibility).
For each earthquake associated with multiple solutions, we compute the average P (and T) axis angle between a given solution i and the others:
 where N is the number of solutions for the selected earthquake, and Pi and Pj are the P axis vectors (in Cartesian coordinates) for the ith and jth solutions (a similar equation is used for the T axis angle). For earthquakes associated with only two solutions, the average angular differences are the same for each solution (diffP1 = diffP2, diffT1 = diffT2) and simply correspond to the difference between the two mechanisms. For earthquakes with more than two solutions, the angular differences of each solution are the average differences with all the others.
where N is the number of solutions for the selected earthquake, and Pi and Pj are the P axis vectors (in Cartesian coordinates) for the ith and jth solutions (a similar equation is used for the T axis angle). For earthquakes associated with only two solutions, the average angular differences are the same for each solution (diffP1 = diffP2, diffT1 = diffT2) and simply correspond to the difference between the two mechanisms. For earthquakes with more than two solutions, the angular differences of each solution are the average differences with all the others.
For all earthquakes associated with multiple solutions, 50% of the P and T angular differences are smaller than 22°, 25% are smaller than 11° and 25% are larger than ca. 40°. Figure 3 shows examples of two earthquakes with four different solutions. For earthquake N = 150 (1980/07/16), the average angular differences of the P axes are small (diffP ≈ 10–20°) for all four solutions, indicating a reasonable agreement in the P axis azimuths and dips. In contrast, the T axis angular differences are significantly larger (diffT ≈ 25–50°) due to the strong disagreement of solution #4 with the other three (Fig. 3a). In comparison, earthquake N = 272 (1985/01/04) has large angular differences (30–70°) for both P and T axes, reflecting the poor agreement between all solutions except the first two and the fact that solutions #3 and #4 are almost diametrically opposite to each other (Fig. 3b).
These angular differences do not provide information on the “right” or “preferred” solution for earthquakes with multiple mechanisms. Only a reanalysis of the signal polarities and the focal mechanism solutions with their specific locations and velocity models would allow discussing their respective quality. However, the angular differences can serve as guidelines when using the database for seismotectonic studies, considering that an earthquake associated with multiple solutions that strongly disagree (differences over 40–50°) should be probably viewed as poorly constrained (unless discussed in the original source). It is worth noting that the opposite may not be true: multiple solutions that strongly agree are not necessarily an indication of robust mechanisms but may simply be due to mechanism inversions performed with the same data and parameters.
 |
Fig. 3 Comparisons of multiple focal mechanism solutions for two example earthquakes. (a) Earthquake N = 150, 1980/07/16, MW = 3.5–4.2 (Mw of original sources). (b) Earthquake N = 272, 1985/01/04, MW = 3.7–4.2 (Mw of original sources). For each solution, the average angular differences with the other three are given above the mechanism (DiffP and DiffT, cf. text). |
4 Regional seismotectonics
In this section, we present short analyses of the FMHex20 database at national and regional scales in order to illustrate how it can help constrain seismotectonic models and seismotectonic zonations for seismic hazard studies. These first-order analyses are based on statistical and spatial distributions of the focal mechanism parameters and comparisons with additional data.
In particular, we compute spatial averages of the faulting styles, orientations of the near-horizontal P axes and orientations of the near-horizontal T axes on a regular grid of spacing d (in km): At each grid point, the averages and standard deviations of these three indicators are computed using all mechanisms within a distance d of the grid point, providing there are at least Nmin mechanisms available (grid points with less than Nmin mechanisms within ± d km are left empty). For the P and T axes orientations, the means and standard deviations are computed for a circular distribution modulo 180° using only near-horizontal axes (dip ≤ 25°). For the faulting style, each focal mechanism is associated with a scalar value S (−1 ≤ S ≤ 1) based on its rake r:
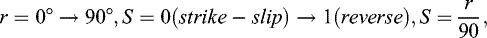
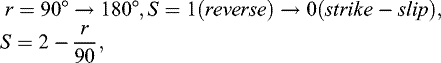


At any grid-point, the average faulting style (obtained by averaging the S values of the different focal mechanism solutions) can be interpreted either as an average fault mechanism defined by multiple earthquakes or as local crustal deformation defined by earthquakes on multiple faults. This interpretation depends on the number, spatial distribution and relation to local faults of the mechanisms used for the grid-point computation (cf. discussion in Section 4.3) and may be biased in regions where deformation styles vary over short distances (e.g., Delacou et al., 2004). A weighting scheme is used in the computation of the grid averages in order to ensure that (1) all earthquakes have the same weight, including those with multiple mechanism solutions, and (2) multiple mechanisms for the same earthquake are weighted based on their compatibility with the others:
-
for earthquakes with only one solution, the mechanism has a weight w = 1;
-
for earthquakes with two solutions, both mechanisms have a weight w = 0.5;
-
for earthquakes with more than two solutions, each mechanism has a weight w ∝ 1 / DiffP + 1 / DiffT (normalized so that the sum of all weights equals 1).
As an example, earthquake N150, 1980/07/16 (Fig. 3a) is associated with four mechanism solutions of faulting styles S = (0.75, 0.74, 0.71, 0.14) and weights w = (0.31, 0.31, 0.20, 0.18), representing the strong similarity of the first two mechanisms versus the dissimilarity of the third and fourth relative to the others. As a result, the first and second mechanisms contribute nearly 2/3 of the weight for this earthquake and the average style is S = 0.62.
4.1 Metropolitan France
The FMHex20 database is shown for the whole metropolitan France and neighboring regions in Figure 4 using four different representations: lower-hemisphere stereographic projections of the focal mechanisms (so called stereonets or “beach balls”, Fig. 4a); average faulting styles (Fig. 4b); average orientations of the P and T axes (Figs. 4c and 4d). At this national scale, we fix the grid spacing/averaging distance to d = 50 km (minimum number of mechanisms Nmin = 4), thus averaging data within a circle of 100 km diameter, in order to highlight significant regional-scale tectonic variations (e.g., inner Alps vs. Alpine foreland distances ca. 50–150 km), while smoothing out the short-scale variability associated with specific faults and structures (few 10 s km).
Average faulting styles in France vary mostly between strike-slip and normal (Fig. 4b). Over two thirds of the distribution correspond to S ≤ 0, with 28% of S ≤ −0.25 (i.e., transtensive to normal). In contrast, transpressive to reverse styles (S ≥ 0.25) represent only 12% of the distribution and are limited to a few areas in western France, the Ardennes, the Alpine forelands and the Ligurian Basin. It is important to note that the grid averaging tends to limit the expression of extreme values (S ≈ −1 or S ≈ 1), especially when very different faulting styles are included in a grid-point computation (this is directly related to the difficulty of defining an average faulting style in cases where normal and reverse mechanisms coexist within a few tens of kilometers). In Figure 4b, the symbol sizes provide a measure of the compatibility of the mechanisms used in the averaging. The smallest symbols correspond to grid points for which the standard deviation of the individual mechanism styles is larger than 0.5, indicating very different mechanisms and an average value that should be analyzed with care before interpretation.
The average orientations of the near-horizontal P and T axes show a strong clustering in the NW-SE and NE-SW quadrants, respectively (Figs. 4c and 4d). Half of the average P axes are oriented N135° ± 30° (SE) whereas only 10% are N45° ± 30° (NE). The clustering is slightly stronger for the average T axis orientations, with more than half (56%) oriented between N45° ± 30° (NE) and only 4% between N135° ± 30° (SE). These overall orientations are consistent with the general pattern of maximum and minimum horizontal compressive stresses (σH and σh) evidenced by in-situ stress data, which indicate average orientations of σH (resp. σh) about NW-SE (resp. NE-SW) for France and most of Western Europe (Paquin et al., 1978; Heidbach et al., 2018; Müller et al., 1992). The Pyrenees and Western Alps are exceptions to this general pattern, with near-horizontal P and T axis orientations showing complex lateral variations along the strike of the orogens (Figs. 4c and 4d).
This overall deformation pattern, and in particular the NW-SE orientation of maximum horizontal compression in a large part of France and neighboring Western Europe can be related to first-order plate tectonic processes, described either in terms of boundary forces such as the mid-Atlantic ridge push and Nubia-Eurasia collision resistance (Gölke and Coblentz, 1996) or in terms of gravitational potential energy from the topography, crust and lithosphere density structures (Camelbeeck et al., 2013; Maury et al., 2014). The reconstitution of local and regional stress from brittle deformation in the European Platform further suggests that this overall NW-SE compression may exist since the Late–Post Miocene period (ca. 4–7 Ma), at least along and near the Alpine Arc (Bergerat, 1987).
Regional variations exist within this overall deformation pattern, such as in southern Western Alps–Provence region where the near horizontal P-axis orientation remains roughly N-S over the whole area whereas the faulting style switches from reverse to normal over ca. 100 km (Figs. 4b and 4c). Interestingly, this focal mechanism P-axis orientation is consistent with horizontal compression derived from Post Miocene fault data in Provence but not in the southern Western Alps (Bergerat, 1987), suggesting the possibility of a present-day forcing mechanism different from plate tectonics in the latter region.
In-depth regional analyses are beyond the scope of this article and would require several specific tasks such as detailed examinations (and potential new computations) of the focal mechanism solutions in order to identify preferred solutions, comparisons with independent data (e.g., local faults, geodetic strain rates), etc. However, we present in the next sections two first-order examples of how focal mechanism analyses can be used to help constrain seismotectonics for seismic hazard zonation in a context of relative data paucity (Western France and Brittany) and for regional tectonics and geodynamics in a case of high data density (example of the Jura-Vosges region). Additional figures and maps are also provided for other regions of metropolitan France (cf. Fig. 4a) in the Supplementary Material (without analysis).
 |
Fig. 4 FMHex20 database for metropolitan France and neighboring regions. (a) Stereographic projections (lower hemisphere) of individual focal mechanisms. Symbol sizes are proportional to magnitudes. White dashed boxes show regional figures in Supplementary Material. (b) Grid-average faulting style. Blue (−1): normal, yellow (0): strike slip, red (1): reverse. Symbol sizes are inversely proportional to standard deviations s (large: σ ≤ 0.25, medium: 0.25 < σ ≤ 0.5, small: σ > 0.5). (c) and (d) Grid-average orientations of near-horizontal P (red) and T (blue) axes. Light-color fan shapes indicate standard deviations σ. |
4.2 Western France
As reviewed in Section 2, the general deformation and stress pattern in Western France (Armorican Massif, Normandy, northwestern Massif Central, cf. Fig. 4) has been characterized in previous studies as a mix of extension and strike-slip deformation regimes, with a maximum horizontal compressive stress oriented NW-SE to NNW-SSE (Amorèse et al., 2000; Delouis et al., 1993; Mazabraud et al., 2005). This pattern is also evidenced in the FMHex20 database, which, for this region, comprises 195 solutions for 185 earthquakes between 1968 and 2019 and ranging in magnitude between Mw = 0.7 and Mw = 5.0. The distributions of faulting styles, P axes and T axes for these mechanisms are shown in Figure 5. A large majority (ca. 80%) of the mechanisms corresponds to normal or strike-slip faulting styles, with only 30 solutions associated with transpressive and reverse styles (S ≥ 0.25, Fig. 5a). The P and T axis distributions confirm this concentration of normal to strike-slip mechanisms with over two thirds of the T axes near-horizontal (dip ≤ 25°) and oriented ca. N065°, whereas the P axes vary between horizontal and vertical with a mean orientation ca. N122° (Figs. 5b and 5c).
For this regional application (and that in Section 4.3), we fix the averaging distance to d = 25 km (Nmin = 2) in order to provide the highest resolution on spatial variability of the deformation styles, while still smoothing out short-scale noise due to individual focal mechanisms. This choice of distance is somewhat arbitrary, but owing to the smoothing effect of the method, results based on distances d = 10–30 km show similar patterns. The spatial distribution of grid averages indicates significant local variations within the overall regional pattern (Fig. 6). In particular, the area on the south side of the southern branch of the South Armorican Shear Zone appears to be dominated by transpressive deformation and stands out in contrast with areas to the south and north, which are consistent with the general transtensive to normal styles (Figs. 6a and 6b). A pocket of local reverse faulting exists in southern Cotentin. In both cases, these local faulting styles are constrained by a small number of mechanisms (15 and 3, respectively) and would require more detailed analyses of individual mechanism solutions to establish their robustness. Similarly, the area between Anger and Poitiers is associated with near-horizontal P and T axis orientations that are nearly orthogonal to the general trends (Figs. 6c and 6d). This observation is also based on few mechanisms and should be confirmed by further investigation.
These simple observations can form the basis of a regional seismotectonic model in which the whole region is dominated by a large-scale stress pattern with a minimum horizontal compressive stress σh oriented about NE-SW and corresponding to the smallest principal stress σ3. Under this stress pattern, preexisting faults, including but not limited to those associated with the South Armorican Shear Zone, tend to be reactivated in a mix of strike-slip and normal faulting (with permutations of the two largest principal stresses σ1 and σ2 between horizontal and vertical along a NW-SE orientation). This overall system accommodates a general NE-SW extension or transtension (Fig. 6). However, a few complex cases may exist, in which the same preexisting structures and faults are locally reactivated in a mix of strike-slip and reverse faulting under variations of local stresses, including drastic permutations between the maximum and minimum horizontal stresses. These smaller areas could be identified as independent seismotectonic zones for seismic hazard analysis (e.g., the elongated zone south of the South Armorican Shear Zone, Figs. 6a and 6b).
 |
Fig. 5 Focal mechanism distributions for Western France. (a) Ternary diagram of focal mechanism faulting styles. Colors indicate the faulting style according to the caption on the sides. (b) and (c) Stereographic projections of the P and T axes. Black dots show individual focal mechanism solutions. The colored background shows the smoothed density distribution of all solutions. |
 |
Fig. 6 Focal mechanism maps for Western France. Symbols as in Figure 4. (a) Stereographic projections (lower hemisphere) of focal mechanisms. (b) Grid-average faulting style. (c) and (d) Grid-average orientations of near-horizontal P and T axes. Orange bars in (c) show in-situ maximum horizontal compressive stress orientations (Paquin et al., 1978). Thin black lines in (a)–(d) show geological and potentially active faults (Baize et al., 2013; Jomard et al., 2017). White dashed ellipses in (a)–(d) show areas of peculiar patterns discussed in the text. SASZ: South Armorican Shear Zone. |
4.3 Northern Alps-Jura-Vosges
In FMHex20, the Northern Alps-Jura-Vosges region (cf. Fig. 4) comprises 501 focal mechanism solutions for 364 individual earthquakes (1954 to 2018, magnitudes 1.7 ≤ Mw ≤ 5.5). The majority of earthquakes is associated with strike-slip to normal faulting styles, with less than 10% of the solutions indicating reverse faulting (Fig. 7a). The P and T axes also show strong concentrations, with T axes mostly horizontal (dip ≤ 25°) with a mean orientation ca. N065° and P axes varying between horizontal and vertical along a mean orientation ca. N133° (Figs. 7b and 7c). This general pattern is consistent with previous studies based on subsets of the FMHex20 database (Delouis et al., 1993; Kastrup et al., 2004). It is also worth noting these general statistics are almost identical to those observed in Western France: same small proportion of reverse faulting styles (10–20%), same average orientations of P and T axes (N120–130° and N065°, respectively), cf. Figure 5 vs. Figure 7.
The regional grid averages (d = 25 km, Nmin = 2) are shown in Figure 8. Over the whole region, the near-horizontal P axis orientations remain remarkably coherent (roughly NW-SE, including across major geological boundaries such as the Jura/Upper Rhine Graben transition), with a 30–50° counter-clockwise rotation from NNE-SSW in the east to ENE-WSW in the south (Figs. 8a and 8c). This general orientation is consistent with that of the maximum horizontal compressive stress measured in boreholes (Paquin et al., 1978; Heidbach et al., 2018). In contrast, the average faulting style shows strong spatial variations: mostly transtensive to normal in the Upper Rhine Graben, Black Forest and western Swiss Alps, versus mostly transpressive to reverse in the central Swiss Alps and south of the Lake Geneva (Fig. 8b). The Jura Mountains also show strong spatial variations in the average faulting style, but these average values are associated with large standard deviations (σ > 0.5) indicating that they are based on very different mechanisms within a small (± 25 km) distance. These would require detailed analyses of the mechanisms in order to study the actual local deformations.
As an example of a possible seismotectonic study using complementary datasets such as geodetic data (e.g., Rabin et al., 2018; Walpersdorf et al., 2018), a comparison is shown in Figure 8d with horizontal Global Positioning System (GPS) strain rates. This example corresponds to a strain rate model derived from GPS velocities smoothed over characteristic distances of ca. 100–200 km (Masson et al., 2019). Assuming that the average mechanism faulting styles and near-horizontal P axis orientations can be interpreted as first-order indicators of crustal deformation and horizontal compression, the comparison with the geodetic strain rates reveals some complex patterns:
-
In the French Jura-northwestern Alps area, the focal mechanisms and geodetic strain rates agree in styles and orientations. Both indicate NW-SE shortening in the Jura, transitioning a dual pattern of E-W transpression and N-S extension in the northwestern Alps (Fig. 8b vs. Fig. 8d).
-
In the central Swiss Alps, Black Forest and Upper Rhine Graben, the agreement is also reasonable between the P axis and geodetic shortening orientations. However, while both datasets indicate shortening in the central Swiss Alps, the geodetic data show strong shortening in the Black Forest and Upper Rhine Graben in contrast with transtension in the focal mechanisms (Fig. 8b vs. Fig. 8d).
This comparison provides a good example of the difficulty in defining a robust seismotectonic model for most of metropolitan France. Due to the very low deformation rates, the datasets are typically limited in size (e.g., number of focal mechanisms) and resolution (e.g., geodetic strain rates). These limitations are added on top of the complexity of the present-day tectonics and dynamic processes at the origin of the deformation and seismicity, such as in the Alpine system where the role of isostatic adjustment to the last glaciation or to ongoing erosion remains debated (Sternai et al., 2019). Such processes may contribute to apparent inconsistencies between geodetic and seismic data (i.e., the former may include large visco-elastic aseismic deformation).
 |
Fig. 7 Focal mechanism distributions for the Northern Alps-Jura-Vosges region. Symbols as in Figure 5. (a) Ternary diagram of focal mechanism faulting styles. (b) and (c) Stereographic projections of the P and T axes. |
 |
Fig. 8 Focal mechanism maps for the Northern Alps-Jura-Vosges region. Symbols as in Figure 4. (a) Stereographic projections (lower hemisphere) of focal mechanisms. (b) Grid average faulting style. (c) Grid-average orientations of near-horizontal P axes. (d) Principal axes of horizontal strain rates from smoothed GNSS data (Masson et al., 2019). Orange bars in (c) show in-situ maximum horizontal compressive stress orientations (Paquin et al., 1978). Thin black lines in (a)–(d) show geological and potentially active faults (Baize et al., 2013; Jomard et al., 2017). White dashed ellipses in (a)–(d) show specific areas discussed in the text. |
5 Conclusion
The FMHex20 database is a compilation of over 1700 focal mechanism solutions for nearly 1300 individual earthquakes in metropolitan France and bordering regions of Western Europe. It is based on published and unpublished sources for which the mechanisms have been verified and corrected for minor errors when required. This first version of the database aims to be the starting point of regular updates as part of the Seismicity Transverse Action of the Résif research infrastructure. These updates may be partly automatic by linking the Résif earthquake bulletin and FMHex database, and partly manual through specific online forms to integrate new research products.
We present first-order analyses of the database for the whole metropolitan France and for a couple of regions taken as examples (Western France and Northern Alps-Jura-Vosges) using statistics and maps of the mechanisms and spatial averages of their parameters (faulting styles, P and T axis orientations). These examples illustrate how the FMHex20 database can be used to construct seismotectonic models and serve as a basis for a variety of projects, from geodynamic studies to zonation for seismic hazard computations. They also highlight the complexity of present-deformation and its driving processes in France. While an overall pattern of NW-SE horizontal compression across the whole territory can be related to classical plate-tectonic processes (e.g., Atlantic ridge push), a variety of other processes, such as isostatic adjustment to erosion or glaciation cycles, are likely at play in different areas (cf. review in Mazzotti et al., 2020). The focal mechanism database combined with complementary datasets (potentially active faults, geodetic strain rates, etc.) can result in better knowledge of the kinematics and slip rates of seismogenic faults, including in areas of low seismicity rates (e.g. Western France) or in regions partly affected by aseismic processes (e.g. glacial isostatic rebound in the Alps).
Supplementary Material
The figures illustrate the distribution and maps of focal mechanisms in the five regions of metropolitan France shown in Figure 4.
Access hereAcknowledgments
This article is part of an ongoing effort of the Seismicity Transverse Action of the Résif research infrastructure (“Réseau Sismologique and Géodésique Français”) to produce and distribute data relating to French seismicity and seismic hazards (https://www.resif.fr/en/actions/transversal-seismicity-action/). We thank Juliette Fabre and Olivier Lobry of the OREME observatory for setting up the online version of the database (https://data.oreme.org/observation/fmhex). Figures, data processing and analysis were made using R (R Core Team, 2019) and GMT 5 (Wessel et al., 2013) software.
References
- Amorèse D, Walker A, Lagarde J-L, Santoire J-P, Volant P, Font M, et al. 2000. New seismotectonic data from an intraplate region: focal mechanisms in the Armorican Massif (northwestern France). Geophysical Journal International 143: 837–846. https://doi.org/10.1046/j.0956-540X.2000.01285.x. [CrossRef] [Google Scholar]
- Baize S, Cushing EM, Lemeille F, Jomard H. 2013. Updated seismotectonic zoning scheme of Metropolitan France, with reference to geologic and seismotectonic data. Bulletin de la Société Géologique de France 184: 225–259. https://doi.org/10.2113/gssgfbull.184.3.225. [CrossRef] [Google Scholar]
- Baroux E, Béthoux N, Bellier O, 2001. Analyses of the stress field in southeastern France from earthquake focal mechanisms. Geophysical Journal International 145: 336–348. [CrossRef] [Google Scholar]
- Bergerat F, 1987. Paleo-champs de contrainte tertiaires dans la plate-forme europeenne au front de l’orogene alpin. Bulletin de la Société Géologique de France III: 611–620. https://doi.org/10.2113/gssgfbull.III.3.611. [CrossRef] [Google Scholar]
- Byerly P, Stauder W. 1958. The Mechanism at the Focus of an Earthquake. Earthquake Notes 29: 17–23. [Google Scholar]
- Camelbeeck T, de Viron O, van Camp M, Kusters D. 2013. Local stress sources in Western Europe lithosphere from geoid anomalies. Lithosphere 5: 235–246. https://doi.org/10.1130/L238.1. [CrossRef] [Google Scholar]
- Cara M, et al. 2015. SI-Hex: a new catalogue of instrumental seismicity for metropolitan France. Bulletin de la Société Géologique de France 186: 3–19. [CrossRef] [Google Scholar]
- Chevrot S, Sylvander M, Delouis B. 2011. A preliminary catalog of moment tensors for the Pyrenees. Tectonophysics 510: 239–251. https://doi.org/10.1016/j.tecto.2011.07.011. [CrossRef] [Google Scholar]
- Cushing EM, Bellier O, Nechtschein S, Sébrier M, Lomax A, Volant P. et al. 2007. A multidisciplinary study of a slow-slipping fault for seismic hazard assessment: the example of the Middle Durance Fault (SE France). Geophysical Journal International 172: 1163–1178. https://doi.org/10.1111/j.1365-246X.2007.03683.x. [CrossRef] [Google Scholar]
- Delacou B, Sue C, Champagnac J-D, Burkhard M. 2004. Present-day geodynamics in the bend of the western and central Alps as constrained by earthquake analysis. Geophysical Journal International 158: 753–774. https://doi.org/10.1111/j.1365-246X.2004.02320.x. [CrossRef] [Google Scholar]
- Delouis B. 2014. FMNEAR: Determination of Focal Mechanism and First Estimate of Rupture Directivity Using Near-Source Records and a Linear Distribution of Point Sources. Bulletin of the Seismological Society of America 104: 1479–1500. https://doi.org/10.1785/0120130151. [CrossRef] [Google Scholar]
- Delouis B, Haessler H, Cisternas A, Rivera L. 1993. Stress tensor determination in France and neighbouring regions. Tectonophysics 221: 413–437. [CrossRef] [Google Scholar]
- Dorel, J, Fréchet, J, Gagnepain-Beyneix, J, Haessler, H, Lachaize, M, Madariaga, R, et al. 1983. Focal mechanism in metropolitan France and the Lesser Antilles. Annales Geophysicae 1: 299–306. [Google Scholar]
- Dziewonski AM, Chou T-A, Woodhouse JH. 1981. Determination of earthquake source parameters from waveform data for studies of global and regional seismicity. Journal of Geophysical Research: Solid Earth 86: 2825–2852. https://doi.org/10.1029/JB086iB04p02825. [CrossRef] [Google Scholar]
- Eva E, Solarino S, Eva C, Neri G. 1997. Stress tensor orientation derived from fault plane solutions in the southwestern Alps. Journal of Geophysical Research: Solid Earth 102: 8171–8185. [CrossRef] [Google Scholar]
- Fréchet J, Pavoni N. 1979. Étude de la sismicité de la zone briançonnaise entre Pelvoux et Argentera (Alpes occidentales) à l’aide d’un réseau de stations portables. Eclogae Geologicae Helvetiae 72: 763–779. [Google Scholar]
- Fréchet J, Thouvenot F, Frogneux M, Deichmann N, Cara M. 2011. The MW 4.5 Vallorcine (French Alps) earthquake of 8 September 2005 and its complex aftershock sequence. Journal of Seismology 15: 43–58. https://doi.org/10.1007/s10950-010-9205-8. [CrossRef] [Google Scholar]
- Gephart JW, Forsyth DW. 1984. An improved method for determining the regional stress tensor using earthquake focal mechanism data: Application to the San Fernando Earthquake Sequence. Journal of Geophysical Research: Solid Earth 89: 9305–9320. https://doi.org/10.1029/JB089iB11p09305. [CrossRef] [Google Scholar]
- Godefroy P. 1980. Apport des mécanismes au foyer à l’étude sismotectonique de la France – un exemple de distribution des contraintes en domaine intraplaque. BRGM 80 SGN 032 GEG 68. [Google Scholar]
- Gölke M, Coblentz DD. 1996. Origins of the European regional stress field. Tectonophysics 266: 11–24. [CrossRef] [Google Scholar]
- Hardebeck JL, Michael AJ. 2004. Stress orientations at intermediate angles to the San Andreas Fault, California. Journal of Geophysical Research: Solid Earth 109. https://doi.org/10.1029/2004JB003239. [Google Scholar]
- Hardebeck JL, Shearer PM. 2002. A New Method for Determining First-Motion Focal Mechanisms. Bulletin of the Seismological Society of America 92: 2264–2276. https://doi.org/10.1785/0120010200. [CrossRef] [Google Scholar]
- Heidbach O, Rajabi M, Cui X, Fuchs K, Müller B, Reinecker J, et al. 2018. The World Stress Map database release 2016: Crustal stress pattern across scales. Tectonophysics 744: 484–498. https://doi.org/10.1016/j.tecto.2018.07.007. [CrossRef] [Google Scholar]
- Hinzen K-G. 2003. Stress field in the Northern Rhine area, Central Europe, from earthquake fault plane solutions. Tectonophysics 377: 325–356. https://doi.org/10.1016/j.tecto.2003.10.004. [CrossRef] [Google Scholar]
- Jomard H, Cushing EM, Palumbo L, Baize S, David C, Chartier T. 2017. Transposing an Active Fault Database into a Seismic Hazard Fault Model for Nuclear Facilities – Part 1: Building a Database of Potentially Active Faults (BDFA) for Metropolitan France. Natural Hazards and Earth System Sciences 17(9): 1573–1784. https://doi.org/10.5194/nhess-17-1573-2017. [CrossRef] [Google Scholar]
- Kastrup U, Zoback ML, Deichmann N, Evans KF, Giardini D, Michael AJ. 2004. Stress field variations in the Swiss Alps and the northern Alpine foreland derived from inversion of fault plane solutions. Journal of Geophysical Research: Solid Earth 109: B01402. https://doi.org/10.1029/92JB00132. [Google Scholar]
- Kostrov VV. 1974. Seismic moment and energy of earthquakes, and seismic flow of rock. Izv Acad Sci USSR Phys Solid Earth 1: 23–40. [Google Scholar]
- Larroque C, Delouis B, Godel B, Nocquet J-M., 2009. Active deformation at the southwestern Alps-Ligurian basin junction (France-Italy boundary): Evidence for recent change from compression to extension in the Argentera massif. Tectonophysics 467: 22–34. https://doi.org/10.1016/j.tecto.2008.12.013. [CrossRef] [Google Scholar]
- Larroque C, Delouis B, Sage F, Régnier M, Béthoux N, Courboulex F. et al. 2016. The sequence of moderate-size earthquakes at the junction of the Ligurian basin and the Corsica margin (western Mediterranean): The initiation of an active deformation zone revealed? Tectonophysics 676: 135–147. https://doi.org/10.1016/j.tecto.2016.03.027. [CrossRef] [Google Scholar]
- Lees JM, 2018. RFOC: Graphics for Spherical Distributions and Earthquake Focal Mechanisms. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- Masson C, Mazzotti S, Vernant P, Doerflinger E. 2019. Extracting small deformation beyond individual station precision from dense GNSS networks in France and Western Europe. Solid Earth 10: 1905–1920. https://doi.org/10.5194/se-10-1905-2019. [CrossRef] [Google Scholar]
- Maury J, Cornet FH, Cara M. 2014. Influence of the lithosphere-asthenosphere boundary on the stress field northwest of the Alps. Geophysical Journal International 199: 1006–1017. https://doi.org/10.1093/gji/ggu289. [CrossRef] [Google Scholar]
- Mazabraud Y, Béthoux N, Guilbert J, Bellier O, 2005. Evidence for short-scale stress field variations within intraplate central-western France. Geophysical Journal International 160: 161–178. https://doi.org/10.2113/gssgfbull.S7-XXII.1.93. [CrossRef] [Google Scholar]
- Mazzotti S, Jomard H, Masson F. 2020. Processes and deformation rates generating seismicity in metropolitan France and conterminous Western Europe. BSGF – Earth Sciences Bulletin 191. https://doi.org/10.1051/bsgf/2020019. [Google Scholar]
- Michael, AJ, 1987. Use of focal mechanisms to determine stress: A control study. Journal of Geophysical Research: Solid Earth 92: 357–368. https://doi.org/10.1029/JB092iB01p00357. [CrossRef] [Google Scholar]
- Müller B, Zoback ML, Fuchs K, Mastin L, Gregesen S, Pavoni N, et al. 1992. Regional patterns of tectonic stress in Europe. Journal of Geophysical Research: Solid Earth 97: 11783–11803. [CrossRef] [Google Scholar]
- Nicolas M, Santoire JP, Delpech PY. 1990. Intraplate seismicity: new seismotectonic data in Western Europe. Tectonophysics 179: 27–53. [CrossRef] [Google Scholar]
- Paquin C, Froidevaux C, Souriau M. 1978. Mesures directes des contraintes tectoniques en France septentrionale. Bulletin de la Société Géologique de France 5: 727–731. [CrossRef] [Google Scholar]
- Perrot J, Arroucau P, Guilbert J, Déverchère J, Mazabraud Y, Rolet J, et al. 2005. Analysis of the Mw 4.3 Lorient earthquake sequence: a multidisciplinary approach to the geodynamics of the Armorican Massif, westernmost France. Geophysical Journal International 162: 935–950. https://doi.org/10.4294/jpe1952.21.415. [CrossRef] [Google Scholar]
- Plenefisch T, Bonjer K-P. 1997. The stress field in the Rhine Graben area inferred from earthquake focal mechanisms and estimation of frictional parameters. Tectonophysics 275: 71–97. https://doi.org/10.1016/S0040-1951(97)00016-4. [CrossRef] [Google Scholar]
- Pondrelli S, Morelli A, Ekström G, Mazza S, Boschi E, Dziewonski AM. 2002. European–Mediterranean regional centroid-moment tensors: 1997–2000. Physics of the Earth and Planetary Interiors 130: 71–101. https://doi.org/10.1016/S0031-9201(01)00312-0. [CrossRef] [Google Scholar]
- R Core Team. 2019. R: A Language and Environment for Statistical Computing. Vienna, Austria: R Foundation for Statistical Computing. [Google Scholar]
- Rabin M, Sue C, Walpersdorf A, Sakic P, Albaric J, Fores B, 2018. Present-Day Deformations of the Jura Arc Inferred by GPS Surveying and Earthquake Focal Mechanisms. Tectonics 37: 3782–3804. https://doi.org/10.1029/2018TC005047. [CrossRef] [Google Scholar]
- Reasenberg P, Oppenheimer DH. 1985. FPFIT, FPPLOT and FPPAGE; Fortran computer programs for calculating and displaying earthquake fault-plane solutions. USGS Open-File Report 85-739 109. [Google Scholar]
- Rigo A, Vernant P, Feigl K, Goula X, Khazaradze G, Talaya J, et al. 2015. Present-day deformation of the Pyrenees revealed by GPS surveying and earthquake focal mechanisms until 2011. Geophysical Journal International 201: 947–964. https://doi.org/10.1093/gji/ggv052. [CrossRef] [Google Scholar]
- Roselli P, Marzocchi W, Mariucci MT, Montone P. 2018. Earthquake focal mechanism forecasting in Italy for PSHA purposes. Geophysical Journal International 212: 491–508. https://doi.org/10.1093/gji/ggx383. [CrossRef] [Google Scholar]
- Rueda J, Mezcua J. 2005. Near-real-time Seismic Moment-tensor Determination in Spain. Seismological Research Letters 76: 455–465. https://doi.org/10.1785/gssrl.76.4.455. [CrossRef] [Google Scholar]
- Scognamiglio L, Magnoni F, Tinti E, Casarotti E. 2016. Uncertainty estimations for moment tensor inversions: the issue of the 2012 May 20 Emilia earthquake. Geophysical Journal International 206: 792–806. https://doi.org/10.1093/gji/ggw173. [CrossRef] [Google Scholar]
- Scognamiglio L, Tinti E, Michelini A. 2009. Real-Time Determination of Seismic Moment Tensor for the Italian Region. Bulletin of the Seismological Society of America 99: 2223–2242. https://doi.org/10.1785/0120080104. [CrossRef] [Google Scholar]
- Stauder SJW. 1962. The Focal Mechanism of Earthquakes. In: Landsberg HE, Mieghem JV, eds. Advances in Geophysics. Elsevier, pp. 1–76. [Google Scholar]
- Sternai P, Sue C, Husson L, Serpelloni E, Becker TW, Willett SD, et al. 2019. Present-day uplift of the European Alps: Evaluating mechanisms and models of their relative contributions. Earth-Science Reviews 190: 589–604. https://doi.org/10.1016/j.earscirev.2019.01.005. [CrossRef] [Google Scholar]
- Stich D, Serpelloni E, de Lis Mancilla F, Morales J. 2006. Kinematics of the Iberia–Maghreb plate contact from seismic moment tensors and GPS observations. Tectonophysics 426: 295–317. https://doi.org/10.1016/j.tecto.2006.08.004. [CrossRef] [Google Scholar]
- Sue C, Thouvenot F, Fréchet J, Tricart P. 1999. Widespread extension in the core of the western Alps revealed by earthquake analysis. Journal of Geophysical Research: Solid Earth 104: 25611–25622. [CrossRef] [Google Scholar]
- Sykes LR. 1967. Mechanism of earthquakes and nature of faulting on the mid-oceanic ridges. Journal of Geophysical Research 72: 2131–2153. [CrossRef] [Google Scholar]
- Sylvander M, Souriau A, Rigo A, Tocheport A, Toutain J-P, Ponsolles C, et al. 2008. The 2006 November, ML = 5.0 earthquake near Lourdes (France): New evidence for NS extension across the Pyrenees. Geophysical Journal International 175: 649–664. https://doi.org/10.1111/j.1365-246X.2008.03911.x. [CrossRef] [Google Scholar]
- Tape W, Tape C. 2012. A geometric setting for moment tensors: A geometric setting for moment tensors. Geophysical Journal International 190: 476–498. https://doi.org/10.1111/j.1365-246X.2012.05491.x. [CrossRef] [Google Scholar]
- Vanneste K, Camelbeeck T, Verbeeck K. 2013. A Model of Composite Seismic Sources for the Lower Rhine Graben, Northwest Europe. Bulletin of the Seismological Society of America 103: 984–1007. https://doi.org/10.1785/0120120037. [CrossRef] [Google Scholar]
- Veinante-Delahaye A, Santoire JP. 1980. Sismicité récente de l’arc sud-armoricain et du nord-ouest du Massif Central. Mécanismes au foyer et tectonique. Bulletin de la Société Géologique de France 7: 93–102. [CrossRef] [Google Scholar]
- Walpersdorf A, Pinget L, Vernant P, Sue C, Deprez A, The RENAG team, 2018. Does Long-Term GPS in the Western Alps Finally Confirm Earthquake Mechanisms? Tectonics 91: 937. https://doi.org/10.1029/96JB03860. [Google Scholar]
- Wessel P, Smith WHF, Scharroo R, Luis J, Wobbe F. 2013. Generic Mapping Tools: Improved Version Released. Eos, Transactions American Geophysical Union 94: 409–410. https://doi.org/10.1002/2013EO450001. [CrossRef] [Google Scholar]
Cite this article as: Mazzotti S, Aubagnac C, Bollinger L, Coca Oscanoa K, Delouis B, Do Paco D, Doubre C, Godano M, Jomard H, Larroque C, Laurendeau A, Masson F, Sylvander M, Trilla A. 2021. FMHex20: An earthquake focal mechanism database for seismotectonic analyses in metropolitan France and bordering regions, BSGF - Earth Sciences Bulletin 192: 10.
All Figures
 |
Fig. 1 Schematic state of stress in France from published focal mechanism inversions. Thick dashed lines with inward-pointing arrows indicate the general direction of maximum horizontal compressive stress for Western Europe (e.g., Heidbach et al., 2018). Small bars show the orientations of maximum horizontal compressive stress from published regional focal mechanism inversions, with the deformation regime indicated in color: green = strike slip, blue = extension, red = shortening. Numbers indicate the reference for the nearest stress indicator: 1 – Baroux et al. (2001); 2 – Mazabraud et al. (2005); 3 – Rigo et al. (2015); 4 – Sue et al., (1999); 5 – Eva et al. (1997); 6 – Delouis et al. (1993); 7 – Hinzen (2003); 8 – Plenefisch and Bonjer (1997); 9 – Rabin et al. (2018). URG and LRG: Upper and Lower Rhine Graben. |
| In the text | |
 |
Fig. 2 Number of focal mechanism solutions per earthquake. Note the logarithmic scale for the frequencies. |
| In the text | |
 |
Fig. 3 Comparisons of multiple focal mechanism solutions for two example earthquakes. (a) Earthquake N = 150, 1980/07/16, MW = 3.5–4.2 (Mw of original sources). (b) Earthquake N = 272, 1985/01/04, MW = 3.7–4.2 (Mw of original sources). For each solution, the average angular differences with the other three are given above the mechanism (DiffP and DiffT, cf. text). |
| In the text | |
 |
Fig. 4 FMHex20 database for metropolitan France and neighboring regions. (a) Stereographic projections (lower hemisphere) of individual focal mechanisms. Symbol sizes are proportional to magnitudes. White dashed boxes show regional figures in Supplementary Material. (b) Grid-average faulting style. Blue (−1): normal, yellow (0): strike slip, red (1): reverse. Symbol sizes are inversely proportional to standard deviations s (large: σ ≤ 0.25, medium: 0.25 < σ ≤ 0.5, small: σ > 0.5). (c) and (d) Grid-average orientations of near-horizontal P (red) and T (blue) axes. Light-color fan shapes indicate standard deviations σ. |
| In the text | |
 |
Fig. 5 Focal mechanism distributions for Western France. (a) Ternary diagram of focal mechanism faulting styles. Colors indicate the faulting style according to the caption on the sides. (b) and (c) Stereographic projections of the P and T axes. Black dots show individual focal mechanism solutions. The colored background shows the smoothed density distribution of all solutions. |
| In the text | |
 |
Fig. 6 Focal mechanism maps for Western France. Symbols as in Figure 4. (a) Stereographic projections (lower hemisphere) of focal mechanisms. (b) Grid-average faulting style. (c) and (d) Grid-average orientations of near-horizontal P and T axes. Orange bars in (c) show in-situ maximum horizontal compressive stress orientations (Paquin et al., 1978). Thin black lines in (a)–(d) show geological and potentially active faults (Baize et al., 2013; Jomard et al., 2017). White dashed ellipses in (a)–(d) show areas of peculiar patterns discussed in the text. SASZ: South Armorican Shear Zone. |
| In the text | |
 |
Fig. 7 Focal mechanism distributions for the Northern Alps-Jura-Vosges region. Symbols as in Figure 5. (a) Ternary diagram of focal mechanism faulting styles. (b) and (c) Stereographic projections of the P and T axes. |
| In the text | |
 |
Fig. 8 Focal mechanism maps for the Northern Alps-Jura-Vosges region. Symbols as in Figure 4. (a) Stereographic projections (lower hemisphere) of focal mechanisms. (b) Grid average faulting style. (c) Grid-average orientations of near-horizontal P axes. (d) Principal axes of horizontal strain rates from smoothed GNSS data (Masson et al., 2019). Orange bars in (c) show in-situ maximum horizontal compressive stress orientations (Paquin et al., 1978). Thin black lines in (a)–(d) show geological and potentially active faults (Baize et al., 2013; Jomard et al., 2017). White dashed ellipses in (a)–(d) show specific areas discussed in the text. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.




