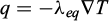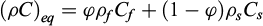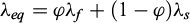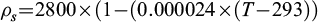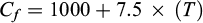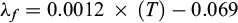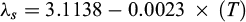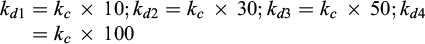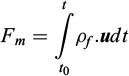| Issue |
BSGF - Earth Sci. Bull.
Volume 195, 2024
|
|
|---|---|---|
| Article Number | 13 | |
| Number of page(s) | 24 | |
| DOI | https://doi.org/10.1051/bsgf/2024010 | |
| Published online | 03 July 2024 | |
Surface-derived fluid percolation along detachment systems enhanced by syn-kinematic granites: uranium mineralization as an application
Percolation des fluides météoriques le long des systèmes de détachement favorisées par la mise en place de granites syn-cinématiques : application aux minéralisations uranifères
1
University of Rennes, CNRS, Geosciences Rennes, UMR 6118, 35000 Rennes, France
2
Goethe University Frankfurt, FB 11, Geosciences Institute, Altenhöferallee 1, 60438 Frankfurt, Germany
* e-mail: khaled.bock@univ-rennes.fr
Received:
15
September
2023
Accepted:
7
May
2024
Detachment zones are privileged areas for the interaction between surface-derived fluids and rocks, potentially leading to ore deposition. However, the hydrodynamics of detachments and specifically the way by which surface-derived fluids reach crustal depths, remain enigmatic. This question is even more puzzling when the heating caused by the emplacement of a syn-kinematic granite increases the buoyancy of fluids, thus impeding their descent. Here, 2D hydrothermal numerical models are performed. The geometry comprises a detachment and secondary normal faults in the hanging wall. Sensitivity tests were carried out to assess the impact of topographic gradients, syn-tectonic magmatic activity and the depth-dependent permeability contrast between the detachment and the crust. Several flow indicators, integrated over time and combined with particle tracking, enable us to highlight the main controls of fluid circulations. Our study reveals that the infiltration of surface-derived fluids into detachment zones is enhanced by the presence of a heat source at depth, such as a syn-kinematic pluton. Secondary faults are the main percolation path for surface-derived fluids infiltrating the detachment. Plume-like thermal anomalies have been spotted between these faults. The dynamic permeabilities of magmatic intrusions, which depend on sub-solidus temperatures, spatially and temporally reproduce the conceptual model of uranium mineralization in the South Armorican Variscan Domain, which is used as an example.
Résumé
Les zones de détachement sont des zones privilégiées pour l’interaction entre les fluides de surface et les roches, ce qui peut conduire à des minéralisations. Cependant, l’hydrodynamique des détachements et plus particulièrement la manière dont les fluides météoriques atteignent des profondeurs crustales restent énigmatiques. Cette question est d’autant plus prégnante lorsque la chaleur émise par la mise en place d’un granite syn-cinématique peut augmenter la flottabilité des fluides, limitant ainsi leur descente. Des modèles numériques hydrothermaux en 2D sont donc réalisés dans cette étude. La géométrie comprend un détachement et des failles normales secondaires localisées à son toit. Des tests de sensibilité ont été menés pour évaluer les effets du gradient topographique, de l’activité magmatique syntectonique, ainsi que du contraste de perméabilité entre le système du détachement et la croûte, avec une perméabilité qui varie avec la profondeur. Plusieurs indicateurs de flux, intégrés dans le temps et combinés au suivi des particules, nous permettent de mettre en évidence les principaux contrôles sur la circulation des fluides. Cette étude révèle que l’infiltration des fluides météoriques dans les zones de détachement est favorisée par la présence d’une source de chaleur en profondeur, telle qu’un pluton syn-cinématique. Les failles secondaires constituent la principale voie de percolation des fluides météoriques qui s’infiltrent dans le détachement. Des anomalies thermiques en forme de panache ont été repérées entre ces failles. Les perméabilités dynamiques des intrusions magmatiques, qui dépendent des températures sub-solidus, reproduisent spatialement et temporellement le modèle conceptuel de la minéralisation de l’uranium dans le domaine varisque sud-armoricain, qui est utilisé comme cas d’application.
Key words: Crustal detachments / meteoric fluids / syn-kinematic granites / depth-dependent and dynamic permeabilities / numerical hydro-thermal coupling / uranium mobility
Mots clés : Détachements crustaux / fluides météoriques / granites syn-cinématiques / perméabilités dynamiques et dépendantes de la profondeur / couplage numérique hydro-thermal / mobilité de l’uranium
© K. Bock et al., Published by EDP Sciences 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Detachments are ductile-to-brittle low-angle normal faults with an initial shallow dip (likely less than 30°), occurring on a sub-regional to regional scale (Armstrong, 1972; Buck, 1988; Davis and Lister, 1988; Platt et al., 2015). They accommodate lower crust exhumation during syn-orogenic thickening and late orogenic thinning (Burg et al., 1984; Whitney et al., 2013; Kellett et al., 2019), mantle exhumation in divergent settings such as slow to ultra-slow oceanic ridges (e.g., McCaig et al., 2007) and hyper-extended margins (e.g., Whitmarsh et al,, 2001). In continental settings, detachments have been mostly studied in late orogenic settings where they give rise to metamorphic core complexes (MCCs, Davis and Lister, 1988). MCCs are characterized by domal geological structures and comprised of deformed high-grade metamorphic rocks (Fig. 1). In the foot wall of detachments, isotherms are upraised, which frequently triggers partial melting. Syn-kinematic plutons also emplace in the foot wall of detachments (Fig. 1, e.g., Crittenden et al., 1980; Daniel and Jolivet, 1995; Smith et al., 2010; Labrousse et al., 2016).
For forty years, fluid-rock-deformation interactions involved in detachment dynamics have received particular attention following three main axes: (i) a hydro-mechanical approach which aims to solve the “mechanical paradox” of initiation, propagation and slow or repeated sliding along detachment (e.g., Sibson, 1985, Sibson 2000; Reynolds and Lister, 1987; Axen, 1992; Collettini, 2011); (ii) a metallogenic approach dedicated to ore systems (e.g., Spencer and Welty 1986; Beaudoin et al., 1991; Smith et al., 1991; Maineri et al., 2003; Menant et al., 2013; Ducoux et al., 2017); (iii) an isotopic approach notably aiming at reconstructing paleo-altitudes in mountain belts (e.g., Chamberlain et al., 2012; Gébelin et al., 2013). Most of these works emphasize the influx of surface-derived fluids along the detachment plane where they mix with upward-circulated crustal (magmatic and metamorphic) fluids (Siebenaller et al., 2013; Dusséaux et al., 2019). Note that, in some cases, only crustal fluids were reported (Famin and Nakashima, 2005; Dyja et al., 2016; Dyja-Person et al., 2018).
In detachment zones, fluid flows are primarily constrained by three factors (Fig. 1): (1) buoyancy (temperature or composition-dependent fluid density), (2) pressure gradients driven by topography, seismic pumping and fluid sources such as surface reservoirs, magmas, exhuming metamorphic rocks and migmatites, and (3) permeability contrasts (Famin et al., 2004; Person et al., 2007; Gottardi et al., 2013). At first order, the challenge of explaining the infiltration of surface-derived fluids to the ductile-brittle transition zone arises as permeability decreases with increasing depth (Manning and Ingebritsen, 1999) and buoyancy forces increase with increasing temperature, especially when syn-kinematic plutons are emplaced in detachments. Downward circulation of surface-derived fluids is thus counterintuitive (e.g., Bons and Gomez-Rivas, 2020). However, in dealing with metal mobilities, it is well-documented that the formation of ore deposits particularly uranium ones, is often linked to the deep percolation (over several kilometers) of oxidizing meteoric fluids along detachment zones (e.g., Kerrich, 1986; Ballouard et al., 2017; Qiu et al., 2018).
In this context, we investigate here the conditions (driving forces, petrophysical properties) under which surface-derived fluids percolate into detachment systems. We then apply the modeling to uranium deposition in relation with crustal detachments, syn-kinematic granites and downward percolation of surface-derived oxidizing fluids. The Rock Alteration Index (RAI), introduced by Philipps (1991) and widely used in numerous studies (e.g. Zhao et al., 1998; Gow et al., 2002; Harcouët-Menou et al., 2009; Eldursi et al., 2009) to pinpoint the potential zones of mineralization, serves as a pivotal parameter for the analysis of this case study.
 |
Fig. 1 Major fluid driving forces involved in continental detachments associated with metamorphic core complexes. Driving forces derived from pressure gradients induced by seismic pumping or valving are not represented. |
2 Modeling strategy and set-up
2.1 Strategy
In this study, fluid flow through porous media within detachment zones was modeled by coupling fluid flow and heat transfer equations, an approach similar to that used in multiple studies (e.g., Duwiquet et al., 2019; Eldursi et al., 2009; Guillou-Frottier et al., 2013; Launay et al., 2023). To investigate the mechanisms responsible for the downward circulation of surface-derived fluids in detachment zones, our strategy includes the following steps (Fig. 2): building of a 2D model using Comsol Multiphysics, which allows (1) testing the impact of topography-driven pressure gradients by including variable differences in the elevation between the foot wall and the hanging wall; (2) testing the effects of a pluton emplacement along the detachment; (3) testing the sensibility of surface-derived fluid flows to depth-dependent permeability contrast between the detachment and the surrounding crust.
From the three tested topography models, one topography configuration was selected to investigate the effect of the emplacement of a pluton, which plays the role of a heat source. Two emplacement depths have been envisaged, a shallow one (≈ 4 km depth for the pluton upper limit) and a deeper one (≈ 10 km depth for the upper limit). The chosen depths of 4 km (e.g., Ballouard et al., 2017) and 10 km (e.g., Simmons and Webber, 2008) for the pluton emplacement aim to capture the range of post-orogenic thermal environments. The shallower depth of 4 km mirrors late-stage intrusions, typical in post-orogenic settings where crustal thinning allows magma to rise closer to the surface. This depth is ideal for studying near-surface thermal effects and hydrothermal processes. Conversely, the deeper emplacement at 10 km reflects early post-orogenic activity when the crust is thicker and retains more heat, which allows studying the thermal influence of the pluton at deeper crustal levels. Then, a decision regarding the pluton position was made to refine the permeability model for the magmatic intrusion by indexing the permeability of the crystallizing magma to temperature. This refers to the pluton dynamic permeability experiments (Fig. 2).
Throughout all these steps, a total of 33 simulations were performed.
 |
Fig. 2 Flowchart depicting the modeling strategy employed, showcasing the four primary tests conducted to examine the effects of topography, pluton, and permeability contrast between the crust and detachment faults. |
 |
Fig. 3 Depth vs. permeability diagram showing the depth-dependent exponential law of the crust (Kc) permeability and the four tested detachment permeability laws (Kd). The pluton non-dynamic permeability model is indicated on the left. |
2.2 Constitutional laws and physical parameters
2.2.1 Governing equations and coupling
2.2.1.1 Heat transfer in porous media
The equation of heat transfer in porous media is used to represent convection-diffusion heat transfer for a single incompressible fluid phase. This equation assumes that the temperatures of the solid and the fluid are instantaneously equilibrated, as indicated by Equation (1). The units for all the parameters presented in the equations are provided in Table 1.
where (ρC)eq is the equivalent volumetric heat capacity at constant pressure, ρfCf is the volumetric heat capacity of the fluid, u is Darcy’s velocity, λeq corresponds to the effective thermal conductivity and Qt represents the total heat source.
The equivalent volumetric heat capacity, denoted by (ρC)eq, as well as the equivalent thermal conductivity are expressed as a volumetric average in the context of a simple fluid-solid mixture as follows:
where s and f stand respectively for solid and fluid, φ is the porosity, ρ is the density, C is the specific heat capacity and λ is the thermal conductivity.
Units and symbols of the used parameters and variables.
2.2.1.2 Fluid flow in porous media
For the simulation of fluid flow through a saturated porous medium, Darcy’s law (Eq. (7)) is employed to describe the fluid velocity within the fluid mass conservation equation (Eq. (6)) for a single incompressible fluid phase.
where u is the Darcy velocity, k represents the intrinsic permeability of the porous medium, µ is the dynamic viscosity of the fluid, p is the pressure and g is the gravitational acceleration. Q is the source term, representing the rate at which fluid volume is being added or removed with respect to time and per unit volume of the porous medium. This source term has been neglected in our modeling as our experiments do not account for processes such as chemical reactions of fluid injection or extraction that would alter the mass of the fluid.
The incompressible fluid flows and heat transfers are coupled through Darcy’s velocity and the fluid density.
2.2.2 Equations of state
2.2.2.1 Density
Fluid density is influenced by both temperature and pressure. The fluid density law (ρf) used here is a polynomial function that fits experimental data for pure liquid water within temperature and pressure ranges of 0–1000 °C and 0–500 MPa (Eq. (8), from Launay, 2018 used in Guillou-Frottier et al., 2020). The solid density (ρs) exhibits a dependency on temperature characterized by a minimal dilatation coefficient (Eq. (9), see Eldursi, 2009). However, in contrast to fluid density, its impact on fluid flow is likely negligible.
2.2.2.2 Specific heat capacity
The equations of state for the specific heat capacity, described in Equations (10) and (11) (Eldursi, 2009), determine the amount of heat absorbed per unit mass of the material (fluid, solid) when temperature increases.
2.2.2.3 Thermal conductivity
Thermal conductivity equations of state presented in Equations (12) and (13) (Eldursi, 2009), describe the intrinsic ability of a material to transfer or conduct heat.
2.2.2.4 Dynamic viscosity
The dynamic viscosity of the fluid as described in Equation (14) is determined by an analytical approximation (Kestin et al., 1978; Rabinowicz et al., 1998) where the effect of pressure is disregarded as proposed by Clauser (2006).
2.2.3 Permeability models
Permeability tends to decrease with depth, following power (Manning and Ingebritsen, 1999) or exponential laws (Saar and Manga, 2004; Garibaldi et al., 2010; Guillou-Frottier et al., 2020). For the sensitivity test of detachment permeabilities (Fig. 2), the permeabilities of the crust and the detachment vary at the same rate but with different orders of magnitude as a function of depth following an exponential law (Eqs. (15), (16) and Fig. 3).
where kc is the crust permeability, kd is the detachment permeability and δ is equal to 3000 m. y represents the altitude expressed in meters with the 0 reference level fixed at the horizontal top of the detachment hanging wall (Figs. 3 and 4). As the foot wall is exhumed by the detachment, the foot wall upper part experienced intense fracturation, hence increasing permeabilities at altitudes above the reference (y > 0). In addition, establishing y = 0 for the flat hanging wall enables consistent comparisons between the three tested topography models (see Sect. 3.3) as they have exactly the same permeability variation from y = 0 (Fig. 3).
Noteworthy, the same permeability law was applied to the detachment and the associated secondary faults affecting the upper plate.
 |
Fig. 4 2D model geometries, boundary and initial conditions with three distinct views: (a) overview of the system showing the three tested topographies and the two pluton positions. At the top, the arrows account for the surface pressure (105 Pa) and temperature (20 °C). The arrows at the bottom correspond to the mean heat flux for the continental crust at the end of the Carboniferous (Jaupart et al., 2015): that period has been selected in order to fit with our application on uranium mineralized detachment systems which formed around 300 Myr in the South Armorican domain (Ballouard et al., 2017). The model size allows assuming no lateral flow with thermal insulation on both the left and right sides. Colored enlargements highlight (b) the topography and detachment thickness near the surface; (c) the mesh resolution in the detachment domain; (d) the two pluton sub-domains. |
2.2.4 Physical indicators
Together with classical parameters such as T, P, mapping of streamlines of Darcy velocities, in order to characterize the fluid flow patterns involved in detachment systems, we calculated additional physical indicators.
2.2.4.1 Peclet number
The Péclet number (Pe) is a dimensionless parameter that corresponds to the ratio of the convective heat flux to the conductive heat flux. In porous media, Equation 17 defines the thermal Pe for a characteristic length (L) (Phillips, 1991; Ingebritsen et al., 2006).
where u is the norm of the u vector and is calculated as  . In the plane defined by the x and y axes, u denotes the horizontal component of the Darcy’s velocity aligned with the x-axis, whereas υ represents the vertical component of Darcy’s velocity in alignment with the y-axis. As we explore potential convection at the scale of the detachment zone, we assumed that L corresponds to the mean detachment thickness (i.e., 700 m) in our models. As a consequence, we particularly tracked Pe greater than 1 (i.e., thermal transfer dominated by fluid advection) along and through the detachment and secondary faults system.
. In the plane defined by the x and y axes, u denotes the horizontal component of the Darcy’s velocity aligned with the x-axis, whereas υ represents the vertical component of Darcy’s velocity in alignment with the y-axis. As we explore potential convection at the scale of the detachment zone, we assumed that L corresponds to the mean detachment thickness (i.e., 700 m) in our models. As a consequence, we particularly tracked Pe greater than 1 (i.e., thermal transfer dominated by fluid advection) along and through the detachment and secondary faults system.
2.2.4.2 Time-integrated fluid flux
The time-integrated fluid flux, denoted by Fm, is a measure of the cumulative amount of fluid mass that has passed through a certain area (a square meter of rock) during a given time period, considering both the fluid density and velocity.
The initial and final instants in year unit are represented by t0 and t, respectively.
2.2.4.3 Fault-parallel fluid velocities (FPFV)
A way to characterize and quantify the fluid flow pattern within and along detachment and secondary faults is to use Darcy’s velocity component parallel to these faults. We thus calculated FPFV using trigonometric projection with a detachment slope of 25° (ud, Eq. (19)) and a 45° dip for the secondary faults (uf, Eq. (20)). Noteworthy, FPFV positive values correspond to upward flowing fluids, whereas negative values indicate downward flowing fluids.
2.2.4.4 Particle tracking
To assess the spatial and temporal dynamics of the surface-derived fluids, we calculated and mapped the pathway of fluid particles originating from various locations at the surface, considering their motion in fluid flow governed by Darcy’s law. For each location, one particle was generated over a series of time increments spanning 100 Kyr. Through time, the same particles have also been tracked in the P-T phase diagram in order to control potential vaporization or to evidence super-critical fluids. Actually, such phase transition has not been documented, which is fortunate because, if it had been the case, it would have implied that the fluid was not incompressible and thus a multiphasic form of the mass and heat conservation should have been used.
2.2.4.5 Restricted rock alteration index (R2AI)
For the application to the uranium mineralization in the detachment context (see dedicated section 6 below), we used a specific indicator, the Rock Alteration Index (RAI). It serves as a useful tool to pinpointing prospective areas of mineralization by identifying the zones where minerals precipitation is likely to occur (Phillips, 1991). Given that the solubility of silicate mineral species increases with temperature, the RAI can be approximated to the scalar product of fluid velocity and temperature gradient (see Eq. (21)). Thus, when fluid flow crosses decreasing isotherms, mineral deposition is favored, and this corresponds to areas where RAI is negative.
Considering that mineralized favorable areas (i.e., ore deposition or strong pervasive hydrothermal alteration) might record high fluid velocities, we extended this RAI parameter by adding a condition on the fluid velocity. Eldursi et al. (2009) proposed a fluid velocity threshold of 10−10 ms−1 considering that this value represents the lower limit of “abnormal velocities”, i.e., one order of magnitude higher than a mean fluid velocity during a bulk regional metamorphic devolatilization. Because our models are slightly more permeable than those of Eldursi et al. (2009), we increased this lower limit to 10−9 m s−1, giving the following formulation for a Restricted RAI (R2AI):
Following the computation of R2AI, our analysis was focused on the selection of regions where R2AI is equal to 1.
2.3 Geometries, boundary and initial conditions
In detachment systems, the thickness of the strain zone can be up to 1.5 km (Whitney et al., 2013), whereas displacement can vary from several kilometers to tens of kilometers (Lister and Davis, 1989; Whitney et al., 2013). In our models, the detachment thickness has been defined as 400 m at the surface and as 1 km at maximum depth (Fig. 4a), this shape of varying thickness with depth was inspired by the detachment models of Reynolds and Lister (1987) and Handy et al. (2007). Near the surface (Fig. 4b), the fault damage zone has been designed asymmetrical, with a greater thickness in the hanging wall than in the foot wall following the conceptual models of Celestino et al. (2020). The dip of a detachment can also influence the development of convection cells, as steeper dips can lead to more rapid and distinct convective patterns over time (Guillou-Frottier et al., 2020). The dip sensitivity of detachment hydrodynamics is not the prime target of this study and thus we opted for a detachment slope of 25°.
In Metamorphic Core Complexes, the hanging wall of detachments is frequently cut by secondary antithetic or synthetic normal faults (Wernicke, 1981; Lister and Davis, 1989). This fault architecture is a first-order control on the hydrodynamics of the system (Reynolds and Lister, 1987). We thus opted for three high-angle antithetic normal faults with a constant dip and a fixed position (Fig. 4a).
The boundary conditions for the simulations depicted in Figure 4 include a surface temperature of 20 °C and a constant heat flux of 37 mW m−2. The lateral boundaries were thermally insulated, and a no-flow condition was applied at the bottom and on both sides. At the surface, a pressure equivalent to atmospheric conditions (P = 105 Pa) was set, with pressure increasing with depth as the initial condition. An initial simulation for a period of 10 Myr during which the detachment was inactive, which means that the detachment domain and the surrounding crust shared similar thermal and hydrodynamic properties. These conditions permitted the establishment of a stable fluid flow, setting the baseline conditions for the models. The models employ a higher resolution mesh in the areas of the detachment and secondary faults, with element sizes ranging from a maximum of 50 m to a minimum of 2 m (Fig. 4c).
2.4 Physical properties, time management and pluton implementation
The models cover a time span of 20 Myr during which the detachment is active (i.e., the detachment has higher permeability than the crust). These models then included both topographical (pressure gradient) and pluton-induced (buoyancy) driving forces for fluid circulation. The elliptical pluton domain is approximately 10 km long and 1 km thick (Fig. 4) in accordance with the pluton geometries and sizes described in the literature (e.g., Guillet et al., 1983; Ballouard et al., 2015, 2017).
The experiments with a pluton can be divided into two groups (Figs. 2 and 3): (1) those with a fixed permeability, designed to examine the effect of the pluton position on hydrodynamics models; (2) those with a pluton dynamic permeability, which investigate the influence of transient magma permeability during crystallization. In both cases, the pluton domain was split into two sub-domains: one within the detachment which represents its apical zone and another one within the crust (Figs. 4a, 4d). This configuration has been used to account for the physical evolution of the injected magma, from the magmatic state to the solid state. Before pluton activation but during detachment working (0–10 Myr), the physical parameters of the pluton crustal sub-domain, among which permeability, are equal to those of the surrounding crust, whereas they are equal to those of the detachment for the pluton sub-domain within the detachment. The heating period (i.e., magma emplacement, from 10 Myr to 11 Myr) is simulated by producing heat of 3.4 × 10−4 W/m3. Similarly to Eldursi et al. (2009), the temperature of the inner part of the pluton was limited below 900 K, which corresponds to the maximum temperature of felsic magmas (Philpotts and Ague, 2009).
In the model considering a pluton dynamic permeability, we took into account the rate of magma crystallization and hence considered permeability changes in response to pluton crystallization. The crystallization rate of a magma is strongly dependent on temperature. From the literature (Bouchez et al., 1992; Fazio et al., 2020), we inferred a 500 °C threshold as the sub-solidus temperature for granitic magmas. Thus, for these specific simulations, we applied the following controls for permeabilities of both pluton sub-domains: in meshes where the temperature was lower than 500°C, the permeability remained equal to those of the crust and the detachment (i.e., solid-state), whereas it dropped to 10−22 m2 when the temperature exceeded 500°C (i.e., magmatic state). At cooling initiation (i.e., 11 Myr), the permeabilities of both pluton sub-domains returned to their initial values (i.e., before activation).
4 Results
4.1 Topography gradient effect
Figure 5 shows the relationships between topography-driven gradient and fluid flow in the detachment zones as seen through the Pe number patterns. In the flat topography model (Fig. 5a), the Pe number is less than 1 for the detachment low permeability model (Kd1, Fig. 5a), no advection of isotherms is visible. With a maximum permeability (Kd4, Fig. 5b), although the Pe number locally exceeds 1 in both the detachment and the secondary faults, the isotherms remain largely undisturbed, which suggests a dominant conductive heat transfer.
In the model with a 500 m topography, for low permeability Kd1 (Fig. 5c), the Pe numbers greater than 1 are restricted to the detachment tip at very shallow depths (less than 2 km). For the Kd4 maximum permeability model Kd4 (Fig. 5d), the Pe numbers greater than 1 are encountered in the upper part of the detachment zone and within the secondary faults. A slight deformation of the isotherms is observed in the hanging wall.
Similar tendencies are observed for the 3000 m topography models (Fig. 5e, Fig 5f), with more pronounced deformation of the isotherms and higher Pe numbers. Experiments (d) and (f) in Figure 5, respectively for the 500 and 3000 m topographies show that some secondary faults (the two deep-rooted ones) localize the downward flow of surface-derived fluids toward the detachment plane, along which they migrate upwards, reaching the shallow-rooted secondary fault along which fluids are discharged toward the surface. For instance, the Kd4 detachment permeability with the 3000 m topography (Fig. 5f) exhibits a discontinuity in the Pe greater than 1 distribution within the detachment segment located between the detachment tip at the surface and the first secondary fault on the right-hand side. This interruption is caused by this secondary fault as it pumps a greater amount of fluids upwards (with Pe exceeding 30, Fig. 5f) causing deformed isotherms by vigorous advection. This fluid flow pattern underlines its convection ability through high permeability localized channels rather than through a matrix of host rocks. Both topography-induced pressure gradients and increasing fault-system permeabilities combine in triggering such convective and channelized fluid flow along high permeabilities fault pathways. Without topography-driven gradient pressure (i.e., flat topography) the whole fault system (detachment and its secondary faults) with high permeability (Kd4, Fig. 5b) behaved as a reservoir in which free thermal and advective flow is possible at depth whereas it is not possible in the surrounding crust. Thus, the fluid flow focused in secondary faults and detachment upper segment may initiate and develop without requiring any topography-driven pressure gradient. On the other side, topographic elevation in the detachment foot wall triggers low velocity and slow diffuse fluid convection in the uppermost permeable crust (see streamlines in Fig. 5). As a result, after several million years, large-scale doming of the isotherms in the lower plate is apparent and is facilitated by high fault system permeabilities (Fig. 5). In turn, this thermal doming exerts positive feedback on high velocity and focused convective fluid flow within fault system.
 |
Fig. 5 Experiments testing the topography effects on surface-derived fluid percolation within the detachment. The snapshots have been taken at the same moment (11.1 Myr). The Pe number greater than 1 (in blue) and isotherms (colored lines) and the major streamlines with arrowheads indicating the flow direction (in purple) are represented for the three tested topographies (0m, 500 m and 3000 m). The three diagrams on the left (a, c, e) correspond to the minimum permeability (Kd1) and those on the right (b, d, f) correspond to the maximum permeability (Kd4). Isotherms are indicated in °C. |
 |
Fig. 6 Shallow pluton emplacement models for two detachment permeability laws Kd3 (left column) and Kd4 (right column). (a) (b): distribution of advective areas (Pe numbers greater than 1) before (9.9 Myr), during (10.5 Myr) and after pluton emplacement (11.1 Myr); (c) (d): isotherms and FPFV in detachment zone and secondary faults for both permeabilities at 11.1 Myr. (e) (f): Close-up at 11.1 Myr showing the streamlines (in purple) and Darcy’s velocity (red arrows, size indexed to velocity value) with the same scale for both permeability laws. |
 |
Fig. 7 Deep pluton emplacement models for two detachment permeability laws Kd3 (left column) and Kd4 (right column). (a) (b): distribution of advective areas (Pe numbers greater than 1) before (9.9 Myr), during (10.5 Myr) and after pluton emplacement (11.1 Myr); (c) (d): isotherms and FPFV in detachment zone and secondary faults for both permeability at 11.1 Myr. (e) (f): Close-up at 11.1 Myr showing the streamlines (in purple) and Darcy’s velocity (red arrows, size indexed to velocity value) with the same scale for both permeability laws. |
4.2 Pluton emplacement effects
4.2.1 Pluton without dynamic permeability
The 500 m topography model has been selected since it strikes a compromise between the flat topography model, which ignores the topography-driven pressure gradient, and the 3000 m model, which exaggerates it.
For the two tested pluton positions, the permeability models Kd1 and Kd2 do not allow a downward flow of meteoric fluids within the detachment fault. Moreover, no convection cells were identified with these detachment permeabilities, implying that within the detachment domain, there is only one direction of fluid flow (upward flow of hot fluids). Therefore, we present models Kd3 and Kd4 in this subsection, for which a downward flow of meteoric fluid in the detachment is predicted.
The Kd3 model (Fig. 6a) exhibits an evolution of the Pe number distribution that witnesses an increase of advective areas during the plutonic activity (10.5 Myr) and after the cooling initiation (11.1 Myr). In both cases, a migration of the Pe numbers higher than 1 from the detachment domain to the hanging wall is observed. Similar patterns are observed for the Kd4 model (Fig. 6b) with higher fluid flow registered by large zones for which Pe numbers higher than 1, particularly near the secondary fault adjacent to the intrusion.
Both permeability models imply a downward flow of surface-derived fluids into two of the secondary faults and into the upper detachment segment. Concurrently, an upward flow of fluids is observed within the secondary fault situated on the far right, extending through the lower segment of the detachment and into the crustal zone above the pluton cupola, where convective patterns develop (Fig. 6e, Fig 6f). Figures 6c and 6d show the thermal regime and fault hydrodynamics during the cooling period, for the two permeability models. The distribution and distortion of the isotherms are roughly similar for both models and present a strong plume-like thermal advective anomaly within the hanging wall. This appears to be controlled and localized by the tip of the shallower secondary fault, located at the far right of the figures, as evidenced by the streamlines in both models (Fig. 6e, Fig 6f). In these models, the ascent of fluid within the lower part of the detachment is hindered by the opposing movement of colder fluids descending along the upper part of the detachment. This obstruction between these two opposite flows forces part of the hot fluids to bypass the detachment domain through the crust domain, forming a plume-like thermal advective anomaly emerging at the surface. Within the detachment itself, the interface between ascending and descending fluid flows is characterized by the formation of intra-detachment semi-complete convection cells (Fig. 6e Fig 6f).
A deeper pluton position induces a contrasting behavior between the two tested permeabilities (Fig. 7). In the Kd3 permeability model, a plume-like thermal anomaly develops above the apical zone of the pluton and beneath the tip of a secondary fault (Fig. 7a, Fig 7c). However, this anomaly vanishes at higher permeabilities (Kd4; Fig. 7b, Fig 7d), with the distribution of Pe numbers higher than 1 being confined to the detachment and secondary faults. This distinct fluid behavior between models Kd3 and Kd4 (Fig. 7) can be attributed to a predominant downward flow within the detachment upper segment in model Kd3 (Fig. 7c, Fig 7e). Subsequently, an upward migration of these fluids occurs in the secondary fault located on the far-left side of the model. However, this upward flow is swiftly redirected from the secondary fault towards the crust, culminating in the formation of the thermal anomaly. This plume-like anomaly is particularly noticeable at the tip of the middle secondary fault, mirroring the thermal anomalies identified in models of the shallower pluton position (Fig. 6c, Fig 7d). On the other hand, fluid flow within the high permeability detachment is unidirectional, ascending only, thus preventing any convection cells to form within the detachment. This is evidenced by the shape of the isotherms and streamlines depicted in Figure 7d and Figure 7f. Interestingly, when there is a significant permeability contrast in the case of a deep magmatic pulse (Fig. 7), the dynamics can shift. Under these conditions, fluid patterns tend to reverse, facilitating downward movement into the hanging wall through the three secondary faults. This mechanism also promotes the evacuation of the fluids towards the surface in the detachment itself. Additionally, we note the formation of a thermal anomaly at the tip of the detachment (Fig. 7d). However, the magnitude of this anomaly is lower than in the other models (Fig. 6c, Fig 6d and Fig. 7c) as we are more distant from the pluton. Comparing shallow and deep pluton emplacement experiments (Fig. 6 and Fig 7), a plume-like anomaly through the crust is generated only when a secondary fault expels fluid upwards. This triggers the possibility for cold fluids to flow downward along the detachment upper segments and then promote by obstruction the by-pass of hot fluids from the detachment to the crust domains. This may occur at great depth (around 10 km in Fig. 7c) where crustal permeability is low (around 10−17 m2).
Thus, drawing upon the principle of mass conservation, the high influx of surface-derived fluids into the pluton emplacement models evidenced by the Pe numbers greater than 1 distribution, streamlines and the isotherms suggests that the formation of the thermal plume-like anomalies serving as exit pathways for the fluids, is highly expected.
 |
Fig. 8 Time-integrated fluid flux estimates for dynamic and fixed permeability models with Kd3 permeability. (a): Time-integrated fluid flux (in log unit) before pluton emplacement, from 9.8 to 9.9 Myr for a 100 Kyr period. (b) and (c): Time-integrated fluid flux (in log unit) during the pluton emplacement (from 10.5 to 10.6 Myr) for non-dynamic and dynamic permeability models of the pluton, respectively. (d) and (e): Zoom in into (b) and (c), respectively. (f) and (g): Profiles of the time-integrated fluid flux (in log unit) and Darcy’s velocity component parallel to the detachment and secondary faults (FPFV) from the AB cross-section, respectively. |
 |
Fig. 9 Pe number vs. detachment permeability models for the two cross-sections (localized as red lines in a). Panels on the left depict the detachment cross-section for the three tested topographies at the same moment (15 Myr, panel b) and for the first pluton position at three different instants (before, during and after its activity) with a topography of 500 m (panel d). On the right, panels c and e display the secondary fault cross-section with conditions identical to panels b and d, respectively. |
4.2.2 Pluton with dynamic permeability
Here, we present results for which the pluton permeability is dynamic (i.e., temperature-dependent): permeability is minimum for the magmatic state and increases with crystallization. As the Kd3 model closely resembles the Kd4 (Fig. 6) and as we are interested in minimalizing the permeability contrast between the crust and the detachment that enables downward percolation, we used the Kd3 detachment permeability law for this simulation. Figure 8 provides, through screenshots and cross-sectional views, a comparative analysis between the pluton model with dynamic permeability and a pluton model with fixed permeability. This comparison focuses on fault-parallel fluid velocities and integrated fluid flux in the detachment system across a 100 Kyr period, examined in three distinct time segments with regard to the stage of pluton activity (i.e., before, during and after emplacement).
In the hanging wall, both models exhibit a correlation between the maximum time-integrated fluid fluxes and the regions where Pe numbers are higher than 1 (Fig. 8b, Fig 8c and Fig 6a). For the pluton dynamic permeability model, an elevated time-integrated fluid flux is discernible in the apical zone of the pluton during both emplacement and cooling (Fig. 8c, Fig 8e and Fig 8f). This increase is one order of magnitude higher than for the phase prior to the pluton activity. 100 Kyr after pluton cooling initiation, the cooling phase is characterized by a symmetry both in time-integrated fluid flux and, more remarkably, in fault-parallel fluid velocities. This apparent symmetry in the FPFV is represented by positive values, denoting upward fluid flow, and negative values, indicating downward fluid flow (Fig. 8g). Such a distribution is consistent with the existence of semi-complete convection cells within the detachment (Fig. 8e), as previously outlined. On the other hand, in the fixed permeability model, fluid flow is significantly lowered during the activation of the pluton due to a decrease in permeability as the plutonic rock is in the magmatic state (Fig. 8b, Fig 8d and Fig 8f). During the cooling phase (11.1 Myr), the positive FPFV values display a unidirectional upward fluid flow (Fig. 8g) which indicates that the semi-convection cells are not present or at least at this cross-section.
4.3 Detachment permeability models with respect to the tested driving forces
In this section, we present a synthesis of our results investigating the topography and plutonic driving forces effect with regard to the four tested detachment permeabilities. Figure 9 presents two cross-sections of a detachment and a secondary fault, displaying the relationship between Pe number and the four tested detachment permeability laws. For the sake of succinctness, only the shallow pluton emplacement model with the three topographical gradient models has been addressed.
Pe numbers less than 1 are observed for all permeability laws in the detachment cross-section with the flat topographical configuration, whereas Pe numbers greater than 1 are observed in three of the detachment permeability laws (Kd2, Kd3, and Kd4) with a 3000 m topography setup (Fig. 9b). With 500 m topography and without magma emplacement at depth, thermal advection within detachment is achieved with a minimum permeability of 50 times the one of the crust (i.e., Kd3). In the secondary fault cross-section (Fig. 9c), for all tested configurations, the Pe numbers increase with the topographical gradients and are nearly constant (i.e., straight horizontal profiles) across the secondary fault (Fig. 9c).
With the pluton (Fig. 9d, Fig 9e) a significant increase in Pe numbers is observed during pluton activity and cooling. Pe numbers are approximately increased by a factor of 2 in the detachment cross-section and by a minimum factor of 4 in the secondary fault cross-section. Notably, during cooling, the detachment exhibits Pe numbers higher than those observed during the pluton activity period. However, in the secondary fault cross-section, these tendencies are reversed as the Pe numbers during the activity period are superior to those of the cooling period. Thus, with a similar topographical configuration (e.g., 500 m in Fig. 9), regardless of the detachment permeability law, pluton emplacement in the detachment enhances thermal advection, which implies vigorous fluid flows in the system.
4.4 Deep percolation of surface-derived fluids within detachment fault systems
Figure 10a depicts the tracking of fluid particles from the surface (close to detachment and secondary faults tips) in the set-up of a shallow pluton with dynamic permeability (i.e., the same experiment as the one presented in Fig 8e, Fig 8d, Fig 8g) during activation of the pluton and the cooling phases (from 10 to 11.1 Myr). According to our results on thermal advection (Fig. 6, Fig 7 and Fig 10), this particle tracking confirms the deep percolation (to a depth ranging from 5 to 11 kilometers, Fig. 10) of surface-derived fluids along the detachment and secondary faults, even though magmas emplaced at depth.
Therefore, if the bulk detachment system, including secondary faults, is considered, several of our simulations reproduce the penetration of meteoric fluid circulations at depth consistently with what is evidenced in many natural detachment cases (e.g., Fricke et al., 1992; Morrison and Anderson, 1998; Dusséaux et al., 2022). Moreover, the tracking of these same particles in a P-T space indicates that, even with a plutonic heat source, fluids remain in a liquid state (e.g., without vaporization, Fig. 10b). This particle tracking does not inform about the amount of surface-derived fluid and thus does not give direct access to the fluid/rock ratio. In further discussion, we thus attempt to evaluate the amount of surface-derived fluids through the analysis of thermal advection and time-integrated fluid fluxes.
 |
Fig. 10 Tracking of fluid particles in (a) a schematic cross-section and in (b) a Pressure-Temperature diagram considering the model with a pluton dynamic permeability. The depth has been approximated following the hydrostatic pressure. The red curve delineates the vapor-liquid transition of pure water according to Cooper and Dooley (2007), with the critical point of pure water (CP) marked by a red dot. |
5 Discussion
5.1 Detachments and fluid circulation in non-magmatic systems
The combination of a high topography and a high permeability ratio between the detachment and the crust creates favorable conditions for meteoric fluid percolation (Fig. 5f), downwelling being assisted by secondary faults in the hanging wall. This pattern has been extensively proposed as a conceptual hydrodynamic model from natural case studies of detachments (Siebenaller et al., 2013; Quilichini et al., 2015; Methner et al., 2015; Gottardi et al., 2011, 2013, 2018). However, buoyancy forces prevent any downward infiltration of meteoric fluids along the detachment plane itself and conceptual models with ascending fluids within detachment (Reynolds and Lister, 1987; Holk and Taylor, 2000) appear to be more coherent with respect to our results. Pe numbers distribution (Fig. 5,Fig 9) coupled with time integrated fluid flux (Fig. 11a) suggest that within a detachment, areas with the highest fluid/rock ratios are limited and restricted to the upper part of the detachment (< 6 km depth).
As our experiments use depth-dependent permeability laws for the crust and the detachment-fault system, our numerical results are difficult to confront directly with results from previous numerical studies dealing with detachment hydrodynamics (e.g., Person et al., 2007; Souche et al., 2014; Roche et al., 2018). However, with a maximum permeability contrast between the detachment and the crust of 100 and a maximum topographic gradient of 3000 m, we do not reproduce advective convection cells within faults and in the hanging wall of detachments (Fig. 5f): Pe numbers are greater than 1 within some faults and detachment segments, but the cooling effects at the intersection between secondary faults and the detachment (Fig 5f and Fig 1, Fig 2, Fig 3, in Fig. 11e) are too low to explain the hanging wall and intra-detachment refrigeration measured in natural cases (Morrison and Anderson, 1998; Famin et al., 2004).
Our models are not designed to simulate fluid flows in supra-detachment sedimentary basins as Souche et al. (2014) have done. In contrast to that study, which ignored topography-induced fluid flows, we do not observe convection cells in the upper plate above the detachment, regardless of the topographies and tested detachment permeabilities (Fig. 5). These contrasting results could be explained by the high initial temperature gradient in the foot wall of Souche et al. (2014) experiments (> 50°C/km).
Internal convection cells within faults and associated convective thermal anomalies are favored by high fault dips (Duwiquet et al., 2019; Guillou-Frottier et al., 2020). Accordingly, our experiments show that a thick detachment (700 m mean) with a low dip (25°) has low potential to developing internal convection cells along with thermal anomalies. This appears to be valid even with a high topographic gradient and high crust-fault permeability contrast. Therefore, convection cells along deep segments of detachments as proposed by Famin et al. (2004) seem unlikely to occur, at least in the absence of pluton emplacement.
 |
Fig. 11 Comparative analysis of detachment zone models with (right side) and without a syn-kinematic pluton (left side). (a) and (b) display the logarithm of time-integrated fluid flux for the two models. (c) and (d) illustrate the FPFV and isotherms. (e) and (f) present the temperature profiles across the detachment cross-section, depicted in (a). |
5.2 Pluton effects on hydrodynamic patterns of detachment systems
Figure 11 shows that the emplacement of a pluton triggers larger and deeper surface-derived fluids percolation along the detachment plane with respect to experiments without magma emplacement. Noteworthy, in natural MCC systems, the magmatic heat zone may also correspond to a migmatitic rock volume. Such “hot” MCC and detachment systems are potentially susceptible to record more vigorous percolation of meteoric water into detachments rather than their “cold” (i.e., magma-poor) equivalent (e.g., Morrison, 1994; Morrison and Anderson, 1998; Gébelin et al., 2011; Siebenaller et al., 2013; Gottardi et al., 2018). Indeed, within the detachment domain, thermal advection and time-integrated fluid fluxes are higher and more widespread than in non-magmatic systems (Fig. 9, Fig. 10 and Fig. 11a, Fig. 11b), suggesting that refrigeration could be more effective in magmatic detachment systems. In particular, the zone of intersections between the secondary normal faults and detachment plane might be preferential zones for recording thermal disequilibrium (Fig. 11f). Our pluton dynamic permeability experiments (Fig 8, Fig 10 and Fig 11) indicate that such localized thermal disequilibrium might be effective within the magmatic bodies themselves.
Our simulations also highlight that detachments associated with magma emplacement may be infiltrated by both ascending and descending fluids at the same time (Fig. 6, Fig 8a and Fig 11a) with complex convection cell-like patterns in the mixing zone (Fig. 6e, Fig 6f). This upward and downward fluid flow is highly sensitive to the depth of the intrusion and the permeability contrast between the crust and the fault. A deep heat source and a permeability contrast greater than 50 appear to stop the coeval upward and downward flows, solely allowing unidirectional ascent of hot fluids in the detachment (Fig. 7d). Such high permeability contrasts might be generated by seismicity with associated hot venting at the detachment tips, a situation described by Famin and Nakashima (2005). Thus, we propose that the hydrodynamic situation we describe may provide important clues when interpreting contrasting isotopic data from the same detachment plane at different depths or across “convection cell-like” segments. Also, these “convection cell-like” areas are zones of fluid mixing and may then be crucial for the decomplexation of dilute species and mineral precipitation.
Using a depth-dependent permeability model for the crust, Eldursi et al. (2009) reproduced akin to what we achieved in our models, namely a plume-like thermal anomaly above a detachment and a pluton simulating the Elba system. Their model does not account for secondary faults nor detachment depth-dependent permeability, suggesting that such anomaly is not triggered by faults in the upper plate. For geothermal and mineral exploration, such anomaly constitutes a valuable target in the context of MCC and active detachments, e.g., the Menderes Massif in Turkey (Roche et al., 2018, 2019). Our study demonstrates that tips of secondary faults in the surface of the upper plate may control the location of such anomaly in case of active magmatism below a low-angle fault zone (Fig. 6 and Fig 7).
Temperature profiles along the detachment segment adjacent to the pluton, illustrate a rapid cooling that commenced at 11 Myr, marked by a significant and immediate temperature drop (Fig. 11f, the 11.1 Myr profile). This initial rapid cooling phase was followed by a more prolonged period of cooling, during which temperatures do not fully return to their pre-emplacement levels (Fig. 11f, the 12 Myr profile). Similar patterns of pluton cooling rates have been observed in the Sierra Nevada batholith, particularly within the John Muir Intrusive Suite (Davis et al., 2012) with the longer cooling period extending to several million years. Pluton cooling rates differ from site to site based on specific conditions, but key factors such as incremental assembly (through successive magma injections), size and depth of emplacement significantly influence these rates (e.g., Simmons and Webber, 2008).
The thermal disequilibrium induced by the magmatic intrusion is still effective 1 Myr after the heat source was stopped, i.e., the magma stopped being injected. This implies that, even with an effective cooling system as the detachment and associated secondary faults, shallow granitic intrusions may propagate long-lived thermal anomaly, more than 1 Myr after the magmatic chamber replenishment.
5.3 Proposed synthetic model
In our study, two sets of conditions allow the deep circulation of surface-derived fluids. The first one corresponds to a high topographical gradient combined with high permeability contrast between detachment/secondary faults and crust (Fig. 5f). The second scenario relies on the presence of a heat source regardless of its position (Fig. 6 and Fig 7) and does not require high permeability contrasts nor a high topographic gradient. Indeed, at least in the upper and middle crust such moderate permeability contrasts may be expected as processes like crack healing and hydrothermal sealing are believed to be rapid (ranging from days to centuries, respectively, according to Gratier, 2011). This would lead to a rapid decrease in fault permeabilities, and thus, a high permeability ratio between the crust and the faults might not be maintained over long durations.
This second scenario emphasizes that high fluxes of surface-derived fluids with detachment are anticipated when magmas are emplaced within the detachment foot wall. This heat source accelerates the fluid movement initiated by the permeability and topography interplay, hence generating faster surface-derived fluids percolation with larger amounts. The secondary faults in the hanging wall also contribute by providing a conduit for these fluids to flow as proposed in many studies (e.g., Reynolds and Lister, 1987; Mulch et al., 2004; Ballouard et al., 2017; Gottardi 2011, 2013, 2018; Qiu et al., 2018).
Topographic gradients facilitate the downward infiltration of such fluids but are not sufficient alone to yield high fluxes (Fig. 12a vs. Fig 12b), even with a permeable secondary fault in the hanging wall. When reconstructing paleo-elevations using stable isotopes, it is essential to consider the hydrodynamic role of magmas on the downward percolation of surface-derived fluids (Fig. 12c). This consideration is crucial to model both late orogenic (e.g., Mulch et al., 2004) and syn-orogenic (e.g., Gébelin et al., 2013) detachments. Detachment systems that incorporate magmatic intrusions are favorable to the downward circulation of surface-derived fluids and are thus able to capture the meteoric isotopic signature, especially in zones of high fluid/rock ratios.
 |
Fig. 12 A proposed synthetic hydrodynamic model of surface-derived fluid circulations along detachment with or without syn-kinematic intrusion. Here we consider an active detachment-fault system creating a moderate permeability contrast (e.g., max ratio of 50) between the crust and the faults. Free topography model proves ineffective in prompting the deep percolation of surface-derived fluids into detachment segment (a). Modest topographic gradients are also insufficient to generate significant fluxes of surface-derived fluids (b). A heat source as a magmatic intrusion in the detachment foot wall enhances such downward fluid fluxes associated with hot upward flows in the hanging wall (c). |
6 Uranium mineralization as an application
Emblematic Variscan U mineralization occurred in relation with detachment activity and syn-kinematic leucogranite emplacement (e.g., the Guérande U-rich system in the South Armorican Domain; Fig. 13; see also Ballouard et al., 2017). Ballouard et al. (2017) have established that the apical zone of the Guérande leucogranite was enriched in U (associated with a Sn mineralization) as a result of concentration of incompatible elements during fractionated crystallization around 310 Myr (Fig. 13c). A new magmatic activity occurred around 300 Myr evidenced by microgranitic dykes (Ballouard et al., 2016, Fig. 13d). Simultaneously, the infiltration of oxidizing meteoric waters along normal faults was responsible for U leaching from the pre-concentrated apical zone (Fig. 13d). Some of these normal faults were active and brittle during the mineralizing stage within the detachment hanging wall (Ballouard, 2016). Uranium precipitated where U-rich fluids came in contact with reducing black shales within the hanging wall.
In this section, we undertake an analysis of a U-mineralized system of Guérande through the use of the dynamic pluton permeability model presented above (Fig. 8). Leucogranitic plutons emplace and cool rapidly (e.g., Petford et al., 2000). Therefore, the main Guérande plutonic body which was emplaced around 310 Myr was crystallized and cooled at 300 Ma. Here, we focus on the magmatic pulse at 300 Myr, which reheated the previously cooled plutonic body. This 300 Myr pulse was accompanied by brittle deformation in the hanging wall. Uranium mineralization was associated with this event (Ballouard et al., 2017). Therefore, during the emplacement period (from 10 to 11 million years), our dynamic pluton permeability model serves as an analog to the magmatic setting of the Guérande system around 300 Myr (Fig. 8c and Fig 13d). The pluton dimensions and its depth of emplacement also match those of the Guérande leucogranite pluton (Guillet et al., 1983). Through this analysis, we thus seek to identify potential zones where uranium could precipitate.
Figure 14 presents the location of the most favorable mineralized zones following our simulations using R2AI mapping. During the activation and the first cooling phases of the pluton (i.e., 10.5 and 11.1 Myr, Fig. 14a and Fig 14b), the detachment itself appears to be of low favorability for mineralization. Rather, the thermal plume-like structure, the apical zone of the pluton and the secondary fault (at least during cooling) exhibit a greater potential for mineral deposition. In this plumbing system where the plume-like structure emerged in the hanging wall, thermal convection (Fig. 8c, Fig 8g) allowed the fluid flow to self-organize into stable patterns with a steep thermal gradient during the period of magmatic activity. As the fluids in this region are heated, they expand and flow faster. This leads to significant fluid movement through the rocks, promoting higher fluid/rock ratios and, consequently, massive solute transfer. This process culminates in the dissolution and transport of dissolved uranium species as Heinrich and Candela (2014) noted, eventually leading to the precipitation and formation of uranium deposits.
In the subsequent cooling phase, in which the thermal anomaly diminishes (between 12 and 12.5 Myr), the isotherms mainly stabilize, adopting a flatter profile, with an exception in the central secondary fault (Fig. 14c, Fig 14d). Within this fault, there is a clear shift in the direction of fluid flow, from a downward direction at 10.5 and 11.1 Myr to an upward direction at 12 and 12.5 Myr. This upward motion fosters a channelized pathway, which has the potential to concentrate the mineralization within the fault zone as indicated by the R2AI (Fig. 14cc and Fig 14d).
In the context of temperature conditions favoring uranium precipitation, Cathelineau (1982) conducted fluid inclusion investigations on quartz combs associated with uranium oxide veins from the Pen Ar Ran deposit. His findings revealed that a low-salinity mineralizing fluid was trapped between 340 °C and 380 °C, at relatively low pressure conditions. Conversely, Ballouard et al. (2017) proposed an alternative explanation, suggesting that the measured high trapping temperatures by Cathelineau (1982) might be exaggerated by radiolytic processes due to uranium decay. They estimated lower trapping temperatures between 250 °C and 350 °C as more accurate, corresponding to local anomalous heat flux.
In our numerical simulations (depicted in Fig. 14a and Fig 14b), we observed an upward circulation of surface-derived heated fluids with temperatures spanning from 200 °C to 360 °C at low-pressure conditions, which mirrors the published physical conditions for the Pen Ar Ran deposit. Furthermore, iterative time-integrated R2AI analysis from magma injection and cooling, indicated that the largest potential for uranium deposition is situated in the hanging wall above the pluton cupola. Thus, the alignment of our modeled conditions with natural observations lends plausibility to the likelihood of uranium precipitation in similar thermal scenarios. It is essential to note that uranium precipitation during an extended cooling period (as shown in Fig. 14c and Fig 14d) is nevertheless unlikely due to the limited amount of surface-derived fluid compared to the period of magmatic activity (Fig. 11 and Fig 12). It remains that the middle secondary fault continues to represent a viable zone for the precipitation of other uranium-bearing minerals such as Coffinite, Autunite and Carnotite that have lower precipitation temperatures.
 |
Fig. 13 Conceptual model showing the main phases of the evolution of uranium mineralization in the Guérande system. (a): Guérande localization in the South Armoricain Domain. (b): Airborne radiometric map showing the distribution of uranium in the Guérande area. (c) Syn-detachment emplacement of the granitic pluton at ca. 310 Myr where the apical zone is enriched in incompatible elements; (d) Exhumation and subsequent brittle deformation at ca. 300 Myr allowing the infiltration of oxidizing meteoric fluids able to leach uranium from the granite and transport uraniferous species along faults. A renewed magmatic activity is recorded at 300 Myr through the leucogranitic dyke emplacement. Precipitation of uraninite occurred along faults crosscutting black shales in the detachment upper plate. Modified after Ballouard et al. (2017) |
 |
Fig. 14 Mapping of potential mineralization zones on the application case of the Guérande U mineralized system through the Restricted Rock Alteration Index (R2AI) at four distinct stages during the activation and cooling phases. Blue arrows indicate downward fluid flow and red arrows indicate upward fluid flow. |
7 Limitations and perspectives
In this study, we conducted 2D hydrodynamic models of detachment zones, exploring several driving forces for the infiltration of surface-derived fluids, including permeability contrast, topography and the role of a heat source. Our findings provide valuable insights regarding the principal determinants that govern the flux of these fluids. Nonetheless, our models do not account for several factors that could potentially influence the hydrodynamics in a detachment zone system. These include: (1) Permeability lateral variation, (e.g., Duwiquet et al., 2019), especially in the detachment zone. Dynamic permeability changes for instance as a function of porosity (e.g., Launay et al., 2023); (2) Seismic pumping which causes an abrupt increase in detachment permeability (e.g., Famin and Nakashima, 2005); (3) 3D modeling investigation which is needed to thoroughly understand the fluid flow pattern and locate plausible convection cells, mainly in the lateral detachment zone section; (4) coupling with chemical reactive transport which is crucial for tracking uranium species speciation, dissolution and precipitation.
8 Conclusion
The present numerical investigation of surface-derived fluids infiltration within detachment zones yields the following conclusions:
In the absence of a pluton, the downward percolation of surface-derived fluids is only achievable under conditions of high topography (≥ 3000 m) coupled with a high detachment/crust permeability ratio (≥ 100).
The emplacement of a pluton along a detachment fault triggers and sustains the downward infiltration of surface-derived fluids, without necessitating a significant permeability ratio contrast nor a steep topography gradient.
Secondary faults within the hanging wall play a pivotal role in stabilizing hydrodynamics by acting as conduits that channel fluid flows from the surface to the detachment zone.
A pluton dynamic permeability indexed to sub-solidus temperature favors large fluid flows and efficient cooling in the apical zone.
Regions conducive to uranium mineralization are consistently identified in the hanging wall, particularly near the leading edge of the pluton.
Acknowledgments
We thank the NEEDS consortium for its funding as part of the URAMOD project, which enabled us to carry out this research. Special thanks go to Laurent Guillou-Frottier and Armel Menant for their constructive reviews, which helped to improve the quality of this work.
References
- Armstrong RL. 1972. Low-Angle (Denudation) Faults, Hinterland of the Sevier Orogenic Belt, Eastern Nevada and Western Utah. Geolog Soc Am Bull 83: 1729. [CrossRef] [Google Scholar]
- Axen GJ. 1992. Pore pressure, stress increase, and fault weakening in low-angle normal faulting. J Geophys Res 97: 8979. [CrossRef] [Google Scholar]
- Ballouard C, Boulvais P, Poujol M, et al. 2015. Tectonic record, magmatic history and hydrothermal alteration in the Hercynian Guérande leucogranite, Armorican Massif, France. Lithos 220-223: 1–22. [Google Scholar]
- Ballouard C, Poujol M, Boulvais P, et al. 2017. Magmatic and hydrothermal behavior of uranium in syntectonic leucogranites: The uranium mineralization associated with the Hercynian Guérande granite (Armorican Massif, France). Ore Geol Rev 80: 309–331. [CrossRef] [Google Scholar]
- Ballouard C. 2016. Origine, évolution et exhumation des leucogranites peralumineux de la chaîne hercynienne armoricaine: implication sur la métallogénie de l’uranium (Doctoral dissertation, Université Rennes 1). [Google Scholar]
- Beaudoin G, Taylor BE, Sangster, DF. 1991. Silver-lead-zinc veins, metamorphic core complexes, and hydrologic regimes during crustal extension. Geology 19: 1217. [CrossRef] [Google Scholar]
- Bons PD, Gomez-Rivas E. 2020. Origin of meteoric fluids in extensional detachments. Geofluids 2020: 1–8. [Google Scholar]
- Bouchez JL, Delas C, Gleizes G, Nédélec A, Cuney M. 1992. Submagmatic microfractures in granites. Geology 20: 35. [CrossRef] [Google Scholar]
- Buck WR. 1988. Flexural rotation of normal faults. Tectonics 7: 959–973. [CrossRef] [Google Scholar]
- Burg JP, Guiraud M, Chen GM, Li GC. 1984. Himalayan metamorphism and deformations in the North Himalayan Belt (southern Tibet, China). Earth Planet Sci Lett 69: 391–400. [CrossRef] [Google Scholar]
- Celestino MAL, Miranda TS de, Mariano G, et al. 2020. Fault damage zones width: Implications for the tectonic evolution of the northern border of the Araripe Basin, Brazil, NE Brazil. J Struct Geol 138: 104116. [CrossRef] [Google Scholar]
- Chamberlain CP, Mix HT, Mulch A, et al. 2012. The Cenozoic climatic and topographic evolution of the western North American Cordillera. Am J Sci 312: 213–262. [CrossRef] [Google Scholar]
- Clauser C. 2006. 8.1 The Earth’s thermal regime. In K. Heinloth (Ed.), Renewable Energy (Vol. 3C, pp. 493–548). Springer Berlin Heidelberg. [CrossRef] [Google Scholar]
- Collettini C. 2011. The mechanical paradox of low-angle normal faults: Current understanding and open questions. Tectonophysics 510: 253–268. [CrossRef] [Google Scholar]
- Cooper JR, Dooley RB. 2007. Revised release on the IAPWS industrial formulation 1997 for the thermodynamic properties of water and steam. Int Assoc Prop Water Steam 1: 48. [Google Scholar]
- Crittenden Jr MD, Coney PJ, Davis GH. 1980. Cordilleran Metamorphic Core Complexes. Geological Society of America Memoirs, vol. 153, 486 p. [Google Scholar]
- Daniel JM, Jolivet L. 1995. Detachment faults and pluton emplacement; Elba Island (Tyrrhenian Sea). Bulletin de La Société Géologique de France 341–354. [CrossRef] [Google Scholar]
- Davis GA, Lister GS. 1988. Detachment faulting in continental extension; Perspectives from the Southwestern U.S. Cordillera. In Geological Society of America Special Papers (Vol. 218, pp. 133–160). Geological Society of America. [CrossRef] [Google Scholar]
- Davis JW, Coleman DS, Gracely JT, Gaschnig R, Stearns M. 2012. Magma accumulation rates and thermal histories of plutons of the Sierra Nevada batholith, CA. Contrib Mineral Petrol 163: 449–465. [CrossRef] [Google Scholar]
- Ducoux M, Branquet Y, Jolivet L, et al. 2017. Synkinematic skarns and fluid drainage along detachments: The West Cycladic Detachment System on Serifos Island (Cyclades, Greece) and its related mineralization. Tectonophysics 695: 1–26. [Google Scholar]
- Dusséaux C, Gébelin A, Boulvais P, et al. 2022. Timing and duration of meteoric water infiltration in the Quiberon detachment zone (Armorican Massif, Variscan belt, France). J Struct Geol 156: 104546. [CrossRef] [Google Scholar]
- Dusséaux C, Gébelin A, Boulvais P, Gardien V, Grimes S, Mulch A. (2019). Meteoric fluid‐rock interaction in Variscan shear zones. Terra Nova, ter. 12392. [Google Scholar]
- Duwiquet H, Arbaret L, Guillou-Frottier L, Heap MJ, Bellanger M. 2019. On the geothermal potential of crustal fault zones: a case study from the Pontgibaud area (French Massif Central, France). Geotherm Energy 7: 33. [CrossRef] [Google Scholar]
- Dyja V, Hibsch C, Tarantola A, et al. 2016. From deep to shallow fluid reservoirs: evolution of fluid sources during exhumation of the Sierra Almagrera, Betic Cordillera, Spain. Geofluids 16: 103–128. [Google Scholar]
- Dyja-Person V, Tarantola A, Richard A, et al. 2018. Metamorphic brines and no surficial fluids trapped in the detachment footwall of a Metamorphic Core Complex (Nevado-Filábride units, Betics, Spain). Tectonophysics 727: 56–72. [CrossRef] [Google Scholar]
- Eldursi K, Branquet Y, Guillou-Frottier L, Marcoux E. 2009. Numerical investigation of transient hydrothermal processes around intrusions: Heat-transfer and fluid-circulation controlled mineralization patterns. Earth Planet Sci Lett 288: 70–83. [CrossRef] [Google Scholar]
- Famin V, Nakashima S. 2005. Hydrothermal fluid venting along a seismogenic detachment fault in the Moresby rift (Woodlark basin, Papua New Guinea): HYDROTHERMAL FLUID VENTING. Geochem Geophys Geosyst 6: (12). [Google Scholar]
- Famin V, Philippot P, Jolivet L, Agard P. 2004. Evolution of hydrothermal regime along a crustal shear zone, Tinos Island, Greece: HYDROTHERMAL REGIME ALONG A SHEAR ZONE. Tectonics 23: (5). [Google Scholar]
- Fazio E, Fiannacca P, Russo D, Cirrincione R. 2020. Submagmatic to solid-state deformation microstructures recorded in cooling granitoids during exhumation of late-Variscan Crust in North-Eastern Sicily. Geosciences 10: 311. [CrossRef] [Google Scholar]
- Fricke HC, Wickham SM, O’Neil JR. 1992. Oxygen and hydrogen isotope evidence for meteoric water infiltration during mylonitization and uplift in the Ruby Mountains-East Humboldt Range core complex, Nevada. Contrib Mineral Petrol 111: 203–221. [CrossRef] [Google Scholar]
- Garibaldi C, Guillou-Frottier L, Lardeaux JM, et al. 2010. Thermal anomalies and geological structures in the Provence basin: Implications for hydrothermal circulations at depth. Bulletin de La Société Géologique de France, 181: 363–376. [CrossRef] [Google Scholar]
- Gébelin A, Mulch A, Teyssier C, Heizler M, Vennemann T, Seaton NCA. 2011. Oligo-Miocene extensional tectonics and fluid flow across the Northern Snake Range detachment system. Nevada: DETACHMENTS AND METEORIC FLUID FLOW. Tectonics 30: n/a-n/a. [Google Scholar]
- Gébelin A, Mulch A, Teyssier C, Jessup MJ, Law RD, Brunel M. 2013. The Miocene elevation of Mount Everest. Geology 41: 799–802. [CrossRef] [Google Scholar]
- Gottardi R, Kao PH, Saar MO, Teyssier C. 2013. Effects of permeability fields on fluid, heat, and oxygen isotope transport in extensional detachment systems: effects of permeability fields. Geochem Geophys Geosyst 14: 1493–1522. [CrossRef] [Google Scholar]
- Gottardi R, Schaper MC, Barnes JD, Heizler MT. 2018. Fluid-rock interaction and strain localization in the Picacho Mountains Detachment Shear Zone, Arizona, USA. Tectonics 37: 3244–3260. [CrossRef] [Google Scholar]
- Gottardi R, Teyssier C, Mulch A, Vennemann TW, Wells ML. 2011. Preservation of an extreme transient geotherm in the Raft River detachment shear zone. Geology 39: 759–762. [CrossRef] [Google Scholar]
- Gow PA, Upton P, Zhao C, Hill KC. 2002. Copper‐gold mineralisation in New Guinea: Numerical modelling of collision, fluid flow and intrusion‐related hydrothermal systems. Austr J Earth Sci 49: 753–771. [CrossRef] [Google Scholar]
- Gratier JP. 2011. Fault permeability and strength evolution related to fracturing and healing episodic processes (years to millennia): the role of pressure solution. Oil Gas Sci Technol 66: 491–506. [CrossRef] [Google Scholar]
- Guillet P, Bouchez JL, Wagner JJ. 1983. Anisotropy of magnetic susceptibility and magmatic structures in the Guérande Granite Massif (France). Tectonics 2: 419–429. [CrossRef] [Google Scholar]
- Guillou-Frottier L, Duwiquet H, Launay G, Taillefer A, Roche V, Link G. 2020. On the morphology and amplitude of 2D and 3D thermal anomalies induced by buoyancy-driven flow within and around fault zones. Solid Earth 11: 1571–1595. [CrossRef] [Google Scholar]
- Handy MR, Hirth G, Hovius N. 2007. Continental Fault Structure and Rheology from the Frictional-to-Viscous Transition Downward. [Google Scholar]
- Harcouët‐Menou V, Guillou‐Frottier L, Bonneville A, Adler PM, Mourzenko V. 2009. Hydrothermal convection in and around mineralized fault zones: Insights from two‐ and three‐dimensional numerical modeling applied to the Ashanti belt, Ghana. Geofluids 9: 116–137. https://doi.org/10.1111/j.1468-8123.2009.00247.x [CrossRef] [Google Scholar]
- Heinrich CA, Candela PA. 2014. Fluids and ore formation in the earth’s crust. In Treatise on Geochemistry (pp. 1–28). Elsevier. [Google Scholar]
- Holk GJ, Taylor HP. 2000. Water as a petrologic catalyst driving 18O/16O homogenization and anatexis of the middle crust in the metamorphic core complexes of British Columbia. Int Geol Rev 42: 97–130. [CrossRef] [Google Scholar]
- Ingebritsen SE, Sanford WE, Neuzil CE. 2006. Groundwater in geologic processes, 2nd ed. Cambridge: Cambridge University Press. [CrossRef] [Google Scholar]
- Jaupart C, Labrosse S, Lucazeau F, Mareschal JC. 2015. Temperatures, heat, and energy in the mantle of the earth. In Treatise on Geophysics (pp. 223–270). Elsevier. [CrossRef] [Google Scholar]
- Kellett DA, Cottle JM, Larson KP. 2019. The South Tibetan detachment system: history, advances, definition and future directions. Geol Soc Lond Spec Publ 483: 377–400. [CrossRef] [Google Scholar]
- Kerrich R. 1986. Fluid infiltration into fault zones: Chemical, isotopic, and mechanical effects. Pure Appl Geophys Pageoph 124: 225–268. [CrossRef] [Google Scholar]
- Kestin J, Khalifa HE, Abe Y, Grimes CE, Sookiazian H, Wakeham WA. 1978. Effect of pressure on the viscosity of aqueous sodium chloride solutions in the temperature range 20-150.degree. C. Journal of Chemical & Engineering Data, 23: 328–336. [CrossRef] [Google Scholar]
- Labrousse L, Huet B, Le Pourhiet L, Jolivet L, Burov E. 2016. Rheological implications of extensional detachments: Mediterranean and numerical insights. Earth Sci Rev 161: 233–258. [CrossRef] [Google Scholar]
- Launay G, Branquet Y, Sizaret S, Guillou-Frottier L, Gloaguen E. 2023. How greisenization could trigger the formation of large vein-and-greisen Sn-W deposits: a numerical investigation applied to the Panasqueira deposit. Ore Geol Rev 153: 105299. [CrossRef] [Google Scholar]
- Launay G. 2018. Hydrodynamique des systèmes minéralisés péri-granitiques: Étude du gisement à W-Sn-(Cu) de Panasqueira (Portugal). Université d’Orléans. [Google Scholar]
- Lister GS, Davis GA. 1989. The origin of metamorphic core complexes and detachment faults formed during Tertiary continental extension in the northern Colorado River region, U.S.A. J Struct Geol 11: 65–94. [CrossRef] [Google Scholar]
- Maineri C, Benvenuti M, Costagliola P, et al. 2003. Sericitic alteration at the La Crocetta deposit (Elba Island, Italy): interplay between magmatism, tectonics and hydrothermal activity. Mineralium Deposita 38: 67–86. [CrossRef] [Google Scholar]
- Manning CE, Ingebritsen SE. 1999. Permeability of the continental crust: implications of geothermal data and metamorphic systems. Rev Geophys 37: 127–150. [CrossRef] [Google Scholar]
- McCaig AM, Cliff RA, Escartin J, Fallick AE, MacLeod CJ. 2007. Oceanic detachment faults focus very large volumes of black smoker fluids. Geology 35: 935. [CrossRef] [Google Scholar]
- Menant A, Jolivet L, Augier R, Skarpelis N. 2013. The North Cycladic Detachment System and associated mineralization, Mykonos, Greece: insights on the evolution of the Aegean domain: Changing stress regime in the Aegean. Tectonics 32: 433–452. [Google Scholar]
- Methner K, Mulch A, Teyssier C, et al. 2015. Eocene and Miocene extension, meteoric fluid infiltration, and core complex formation in the Great Basin (Raft River Mountains, Utah). Tectonics 34: 680–693. [CrossRef] [Google Scholar]
- Morrison J, Anderson JL. 1998. Footwall refrigeration along a detachment fault: implications for the thermal evolution of core complexes. Science 279: 63–66. [CrossRef] [Google Scholar]
- Morrison J. 1994. Meteoric water-rock interaction in the lower plate of the Whipple Mountain metamorphic core complex, California. J Metamorph Geol 12: 827–840. [CrossRef] [Google Scholar]
- Mulch A, Teyssier C, Cosca MA, Vanderhaeghe O, Vennemann TW. 2004. Reconstructing paleoelevation in eroded orogens. Geology 32: 525. [CrossRef] [Google Scholar]
- Person M, Mulch A, Teyssier C, Gao Y. 2007. Isotope transport and exchange within metamorphic core complexes. Am J Sci 307: 555–589. [CrossRef] [Google Scholar]
- Petford N, Cruden AR, McCaffrey KJW, Vigneresse JL. 2000. Granite magma formation, transport and emplacement in the Earth’s crust. Nature 408: 669–673. [CrossRef] [Google Scholar]
- Phillips OM. 1991. Flow and reactions in permeable rocks. Cambridge: Cambridge University Press. [Google Scholar]
- Philpotts AR, Ague JJ. 2009. Principles of igneous and metamorphic petrology, 2nd ed. Cambridge: Cambridge University Press. [CrossRef] [Google Scholar]
- Platt JP, Behr WM, Cooper FJ. 2015. Metamorphic core complexes: windows into the mechanics and rheology of the crust. J Geolog Soc 172: 9–27. [CrossRef] [Google Scholar]
- Qiu L, Yan DP, Ren M, et al. 2018. The source of uranium within hydrothermal uranium deposits of the Motianling mining district, Guangxi, South China. Ore Geol Rev 96: 201–217. [CrossRef] [Google Scholar]
- Quilichini A, Siebenaller L, Nachlas WO. 2015. Infiltration of meteoric fluids in an extensional detachment shear zone (Kettle dome, WA, USA): how quartz dynamic recrystallization relates to fluid-rock interaction. J Struct Geol 71: 71–85. [CrossRef] [Google Scholar]
- Rabinowicz M, Boulègue J, Genthon P. 1998. Two- and three-dimensional modeling of hydrothermal convection in the sedimented Middle Valley segment, Juan de Fuca Ridge. Journal of Geophysical Research: Solid Earth, 103: 24045–24065. [CrossRef] [Google Scholar]
- Reynolds SJ, Lister GS. 1987. Structural aspects of fluid-rock interactions in detachment zones. Geology 15: 362. [CrossRef] [Google Scholar]
- Roche V, Bouchot V, Beccaletto L, et al. 2019. Structural, lithological, and geodynamic controls on geothermal activity in the Menderes geothermal Province (Western Anatolia, Turkey). Int J Earth Sci 108: 301–328. [CrossRef] [Google Scholar]
- Roche V, Sternai P, Guillou-Frottier L, et al. 2018. Emplacement of metamorphic core complexes and associated geothermal systems controlled by slab dynamics. Earth Planet Sci Lett 498: 322–333. [CrossRef] [Google Scholar]
- Saar MO, Manga M. 2004. Depth dependence of permeability in the Oregon Cascades inferred from hydrogeologic, thermal, seismic, and magmatic modeling constraints: Depth dependence of permeability. Journal of Geophysical Research: Solid Earth, 109(B4). [Google Scholar]
- Sibson RH. 1985. A note on fault reactivation. J Struct Geol 7: 751–754. [CrossRef] [Google Scholar]
- Sibson RH. 2000. Fluid involvement in normal faulting. J Geodyn 29: 469–499. [CrossRef] [Google Scholar]
- Siebenaller L, Boiron MC, Vanderhaeghe O, et al. 2013. Fluid record of rock exhumation across the brittle-ductile transition during formation of a Metamorphic Core Complex (Naxos Island, Cyclades, Greece): Fluid record in Naxos metamorphic core complex. J Metamorphic Geol 31: 313–338. [CrossRef] [Google Scholar]
- Simmons WmBS, Webber KL. 2008. Pegmatite genesis: state of the art. Eur J Mineral 20: 421–438. [CrossRef] [Google Scholar]
- Smith BM, Reynolds SJ, Day HW, Bodnar RJ. 1991. Deep-seated fluid involvement in ductile-brittle deformation and mineralization, South Mountains metamorphic core complex, Arizona. Geolog Soc Am Bull 103: 559–569. [CrossRef] [Google Scholar]
- Smith SAF, Holdsworth RE, Collettini C. 2010. Interactions between low-angle normal faults and plutonism in the upper crust: Insights from the Island of Elba, Italy. Geological Society of America Bulletin. [Google Scholar]
- Souche A, Dabrowski M, Andersen TB. 2014. Modeling thermal convection in supradetachment basins: Example from western Norway. Geofluids 14: 58–74. [CrossRef] [Google Scholar]
- Spencer JE, Welty JW. 1986. Possible controls of base- and precious-metal mineralization associated with Tertiary detachment faults in the lower Colorado River trough, Arizona and California. Geology 14: 195. [Google Scholar]
- Wernicke B. 1981. Low-angle normal faults in the Basin and Range Province: Nappe tectonics in an extending orogen. Nature 291: 645–648. [CrossRef] [Google Scholar]
- Whitmarsh RB, Manatschal G, Minshull TA. 2001. Evolution of magma-poor continental margins from rifting to seafloor spreading. Nature 413: 150+. [CrossRef] [Google Scholar]
- Whitney DL, Teyssier C, Rey P, Buck WR. 2013. Continental and oceanic core complexes. Geolog Soc Am Bull 125: 273–298. [CrossRef] [Google Scholar]
- Zhao C, Hobbs BE, Mühlhaus HB. 1998. Finite element modelling of temperature gradient driven rock alteration and mineralization in porous rock masses. Comput Methods Appl Mech Eng 165: 175–187. [CrossRef] [Google Scholar]
Cite this article as: Bock K, Branquet Y, Boulvais P, Duretz T. 2024. Surface-derived fluid percolation along detachment systems enhanced by syn-kinematic granites: uranium mineralization as an application, BSGF - Earth Sciences Bulletin 195: 13.
All Tables
All Figures
 |
Fig. 1 Major fluid driving forces involved in continental detachments associated with metamorphic core complexes. Driving forces derived from pressure gradients induced by seismic pumping or valving are not represented. |
| In the text | |
 |
Fig. 2 Flowchart depicting the modeling strategy employed, showcasing the four primary tests conducted to examine the effects of topography, pluton, and permeability contrast between the crust and detachment faults. |
| In the text | |
 |
Fig. 3 Depth vs. permeability diagram showing the depth-dependent exponential law of the crust (Kc) permeability and the four tested detachment permeability laws (Kd). The pluton non-dynamic permeability model is indicated on the left. |
| In the text | |
 |
Fig. 4 2D model geometries, boundary and initial conditions with three distinct views: (a) overview of the system showing the three tested topographies and the two pluton positions. At the top, the arrows account for the surface pressure (105 Pa) and temperature (20 °C). The arrows at the bottom correspond to the mean heat flux for the continental crust at the end of the Carboniferous (Jaupart et al., 2015): that period has been selected in order to fit with our application on uranium mineralized detachment systems which formed around 300 Myr in the South Armorican domain (Ballouard et al., 2017). The model size allows assuming no lateral flow with thermal insulation on both the left and right sides. Colored enlargements highlight (b) the topography and detachment thickness near the surface; (c) the mesh resolution in the detachment domain; (d) the two pluton sub-domains. |
| In the text | |
 |
Fig. 5 Experiments testing the topography effects on surface-derived fluid percolation within the detachment. The snapshots have been taken at the same moment (11.1 Myr). The Pe number greater than 1 (in blue) and isotherms (colored lines) and the major streamlines with arrowheads indicating the flow direction (in purple) are represented for the three tested topographies (0m, 500 m and 3000 m). The three diagrams on the left (a, c, e) correspond to the minimum permeability (Kd1) and those on the right (b, d, f) correspond to the maximum permeability (Kd4). Isotherms are indicated in °C. |
| In the text | |
 |
Fig. 6 Shallow pluton emplacement models for two detachment permeability laws Kd3 (left column) and Kd4 (right column). (a) (b): distribution of advective areas (Pe numbers greater than 1) before (9.9 Myr), during (10.5 Myr) and after pluton emplacement (11.1 Myr); (c) (d): isotherms and FPFV in detachment zone and secondary faults for both permeabilities at 11.1 Myr. (e) (f): Close-up at 11.1 Myr showing the streamlines (in purple) and Darcy’s velocity (red arrows, size indexed to velocity value) with the same scale for both permeability laws. |
| In the text | |
 |
Fig. 7 Deep pluton emplacement models for two detachment permeability laws Kd3 (left column) and Kd4 (right column). (a) (b): distribution of advective areas (Pe numbers greater than 1) before (9.9 Myr), during (10.5 Myr) and after pluton emplacement (11.1 Myr); (c) (d): isotherms and FPFV in detachment zone and secondary faults for both permeability at 11.1 Myr. (e) (f): Close-up at 11.1 Myr showing the streamlines (in purple) and Darcy’s velocity (red arrows, size indexed to velocity value) with the same scale for both permeability laws. |
| In the text | |
 |
Fig. 8 Time-integrated fluid flux estimates for dynamic and fixed permeability models with Kd3 permeability. (a): Time-integrated fluid flux (in log unit) before pluton emplacement, from 9.8 to 9.9 Myr for a 100 Kyr period. (b) and (c): Time-integrated fluid flux (in log unit) during the pluton emplacement (from 10.5 to 10.6 Myr) for non-dynamic and dynamic permeability models of the pluton, respectively. (d) and (e): Zoom in into (b) and (c), respectively. (f) and (g): Profiles of the time-integrated fluid flux (in log unit) and Darcy’s velocity component parallel to the detachment and secondary faults (FPFV) from the AB cross-section, respectively. |
| In the text | |
 |
Fig. 9 Pe number vs. detachment permeability models for the two cross-sections (localized as red lines in a). Panels on the left depict the detachment cross-section for the three tested topographies at the same moment (15 Myr, panel b) and for the first pluton position at three different instants (before, during and after its activity) with a topography of 500 m (panel d). On the right, panels c and e display the secondary fault cross-section with conditions identical to panels b and d, respectively. |
| In the text | |
 |
Fig. 10 Tracking of fluid particles in (a) a schematic cross-section and in (b) a Pressure-Temperature diagram considering the model with a pluton dynamic permeability. The depth has been approximated following the hydrostatic pressure. The red curve delineates the vapor-liquid transition of pure water according to Cooper and Dooley (2007), with the critical point of pure water (CP) marked by a red dot. |
| In the text | |
 |
Fig. 11 Comparative analysis of detachment zone models with (right side) and without a syn-kinematic pluton (left side). (a) and (b) display the logarithm of time-integrated fluid flux for the two models. (c) and (d) illustrate the FPFV and isotherms. (e) and (f) present the temperature profiles across the detachment cross-section, depicted in (a). |
| In the text | |
 |
Fig. 12 A proposed synthetic hydrodynamic model of surface-derived fluid circulations along detachment with or without syn-kinematic intrusion. Here we consider an active detachment-fault system creating a moderate permeability contrast (e.g., max ratio of 50) between the crust and the faults. Free topography model proves ineffective in prompting the deep percolation of surface-derived fluids into detachment segment (a). Modest topographic gradients are also insufficient to generate significant fluxes of surface-derived fluids (b). A heat source as a magmatic intrusion in the detachment foot wall enhances such downward fluid fluxes associated with hot upward flows in the hanging wall (c). |
| In the text | |
 |
Fig. 13 Conceptual model showing the main phases of the evolution of uranium mineralization in the Guérande system. (a): Guérande localization in the South Armoricain Domain. (b): Airborne radiometric map showing the distribution of uranium in the Guérande area. (c) Syn-detachment emplacement of the granitic pluton at ca. 310 Myr where the apical zone is enriched in incompatible elements; (d) Exhumation and subsequent brittle deformation at ca. 300 Myr allowing the infiltration of oxidizing meteoric fluids able to leach uranium from the granite and transport uraniferous species along faults. A renewed magmatic activity is recorded at 300 Myr through the leucogranitic dyke emplacement. Precipitation of uraninite occurred along faults crosscutting black shales in the detachment upper plate. Modified after Ballouard et al. (2017) |
| In the text | |
 |
Fig. 14 Mapping of potential mineralization zones on the application case of the Guérande U mineralized system through the Restricted Rock Alteration Index (R2AI) at four distinct stages during the activation and cooling phases. Blue arrows indicate downward fluid flow and red arrows indicate upward fluid flow. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.